K A Tsokos Solutions for Chapter: Circular Motion and Gravitation, Exercise 2: Test yourself

The mass of the Moon is about $81$ times less than that of the Earth. Estimate the fraction of the distance from the Earth to the Moon where the gravitational field strength is zero. (Take into account the Earth and the Moon only.)

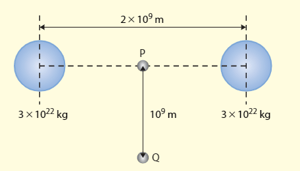
The diagram shows point $\mathrm{P}$ is halfway between the centres of two equal spherical masses that are separated by a distance of $2\times {10}^9\mathrm{m}$ Calculate the gravitational field strength at a point $\mathrm{P}$ and state the direction of the gravitational field strength at point $\mathrm{Q}$.

A satellite orbits the earth above the equator with a period equal to $24 \mathrm{hrs}.$ Determine the height of the satellite above the earth.

[$\mathrm{G}=\left(6.67 {\mathrm{m}}^3{\mathrm{kg}}^{-1}{\mathrm{s}}^{-2}\right)$]

A satellite orbits the earth above the equator with a period equal to $24 \mathrm{hrs}.$ Suggest an advantage of such a satellite.

The Hubble Space Telescope is in the orbit around the earth at a height of $560 \mathrm{km}$ above the earth's surface Calculate the Hubble's speed.

$\left[\mathrm{G}=6.67 {\mathrm{m}}^3{\mathrm{kg}}^{-1}{\mathrm{s}}^{-2}\right]$

In a servicing mission, a space shuttle spotted the Hubble telescope a distance of $10 \mathrm{km}$. Estimate how long it took the shuttle to catch up with the Hubble, assuming that the Shuttle was moving in a circular orbit just $500 \mathrm{m}$ below Hubble's orbit of $560 \mathrm{km}$.

$\left[\mathrm{G}=6.67\times {10}^{-11}{\mathrm{m}}^3{\mathrm{kg}}^{-1}{\mathrm{s}}^{-2}\right]$

Assume that the force of gravity between two point masses is given by $\mathrm{F}=\mathrm{G}\frac{{\mathrm{m}}_1 {\mathrm{m}}_2}{{\mathrm{r}}^{\mathrm{n}}}$, where $\mathrm{n}$ is a constant. Derive the law relating period to orbit radius for this force,

Assume that the force of gravity between two point masses is given by $\mathrm{F}=\mathrm{G}\frac{{\mathrm{m}}_1 {\mathrm{m}}_2}{{\mathrm{r}}^{\mathrm{n}}}$,  Deduce the value of $\mathrm{n}$ if this law is to be identical with Kepler's third law.