K K Sharma Solutions for Chapter: Electromagnetic Induction, Exercise 13: Self Inductance
K K Sharma Physics Solutions for Exercise - K K Sharma Solutions for Chapter: Electromagnetic Induction, Exercise 13: Self Inductance
Attempt the practice questions on Chapter 3: Electromagnetic Induction, Exercise 13: Self Inductance with hints and solutions to strengthen your understanding. Chapterwise/Topicwise Daily Practice Problems (DPP) Magnetism and Electromagnetic Induction NEET solutions are prepared by Experienced Embibe Experts.
Questions from K K Sharma Solutions for Chapter: Electromagnetic Induction, Exercise 13: Self Inductance with Hints & Solutions
A wire of fixed length is wound in such a way that it forms a solenoid of length and radius . Its self inductance is found to be . Now, if the same wire is wound in such a way that it forms a solenoid of length and radius , then the self inductance will be
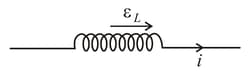
At a given instant, the current and self-induced emf, in an inductor, are directed as shown in the figure. If the induced emf is and the rate of change of current is , then the correct statement is,
The number of turns, cross-sectional area and length for four solenoids are given in the following table.
| Solenoid | Total Turns | Area | Length |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
The solenoid with maximum self inductance is
Two coils are made of copper wires, of the same length. In the first coil, the number of turns is and radius is . In the second coil, the number of turns is and radius is . The ratio of self inductances of these coils will be
For a solenoid, keeping its turn density constant, if its length is halved and its cross-sectional radius is doubled, then, the inductance of the solenoid increases by
When the current in a certain inductor coil is and is increasing at the rate of , the potential difference across the coil is . When the current is and is decreasing at the rate of , the potential difference is . The self inductance of the coil is
The equivalent inductance of two inductance is , when connected in parallel and , when connected in series. The difference between the two inductance is
A superconducting loop of radius has self inductance . A uniform and constant magnetic field is applied perpendicular to the plane of the loop. Initially, the current in this loop is zero. The loop is rotated by about its diameter. The current in the loop, after rotation, is equal to
