Karen Morrison and Nick Hamshaw Solutions for Exercise 5: Exercise 13.5

Calculate upper and lower bounds for the length of the hypotenuse. The two short sides of a right-angled triangle are $3.7$cm (to nearest mm) and $4.5$cm (to nearest mm). Give your answers to the nearest cm. 

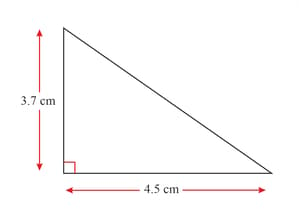
Calculate upper and lower bounds for $x$.The angles in a triangle are $x°, 38.4°$ (to $1 d.p.$) and $78.1°$ (to $1 d.p.$).

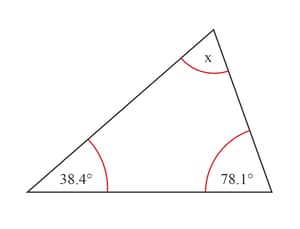
Calculate upper and lower bounds for $x$ as a percentage of $y$ to $1$ decimal place.Quantity $x$ is $45$ to the nearest integer. Quantity $y$ is $98$ to the nearest integer.  

The following five masses are given to $3$ significant figures. Calculate upper and lower bounds for the mean of these masses. 

$138$kg, $94.5$ kg, $1090$ kg ,$345$ kg, $0.354$ kg

Gemma is throwing a biased die. The probability that she throws a five is $0.245$ to $3$ decimal places. Calculate upper and lower bounds for the number of fives Gemma expects to throw, if Gemma throws the die exactly $480$ times. Give your answer to $2$ decimal places. 
 

A cuboid of height $h$ has a square base of side length $a$. In an experiment $a$ and $h$ are measured as $4 cm$ and $11 cm$ respectively, each measured to the nearest $cm$. What are the minimum and maximum possible values of the volume in $c{m}^3$?

A cuboid of height $h$ has a square base of side length $a$. In an experiment, the volume of the block is found to be $350 c{m}^3$, measured to the nearest $50 c{m}^3$, and its height is measured as $13.5 cm$, to the nearest $0.5 cm$. What is the maximum and minimum possible values of the length $a$, in centimetres?

A cuboid of height $h$ has a square base of side length $a$. In an experiment, the volume of the block is found to be $350 c{m}^3$, measured to the nearest $50 c{m}^3$, and its height is measured as $13.5 cm$, to the nearest $0.5 cm$. How many significant figures should be used to give a reliable answer for the value of $a$?