Lynn Byrd, Greg Byrd and, Chris Pearce Solutions for Chapter: Shapes and Symmetry, Exercise 2: Exercise 8.1
Lynn Byrd Mathematics Solutions for Exercise - Lynn Byrd, Greg Byrd and, Chris Pearce Solutions for Chapter: Shapes and Symmetry, Exercise 2: Exercise 8.1
Attempt the practice questions on Chapter 8: Shapes and Symmetry, Exercise 2: Exercise 8.1 with hints and solutions to strengthen your understanding. Cambridge Lower Secondary Mathematics Learner's Book 7 Second Edition Digital Access solutions are prepared by Experienced Embibe Experts.
Questions from Lynn Byrd, Greg Byrd and, Chris Pearce Solutions for Chapter: Shapes and Symmetry, Exercise 2: Exercise 8.1 with Hints & Solutions
Complete the table to show the symmetry properties of these quadrilateral.
| Shape | square | rectangle | rhombus | parallelogram | kite | trapezium | Isosceles trapezium |
| Number of lines of symmetry | |||||||
| Order of rotational symmetry |

Add one blue square to the pattern to make a new pattern that has a line of symmetry. Draw the line of symmetry of the new pattern. Describe the line of symmetry; that is, the line is a vertical, horizontal or diagonal line of symmetry.

Add one blue square to the pattern to make a new pattern that has a line of symmetry. Draw the line of symmetry of the new pattern. Describe the line of symmetry; that is, the line is a vertical, horizontal or diagonal line of symmetry.
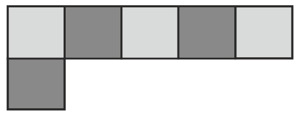
Add one blue square to the pattern to make a new pattern that has a line of symmetry. Draw the line of symmetry of the new pattern. Describe the line of symmetry; that is, the line is a vertical, horizontal or diagonal line of symmetry.
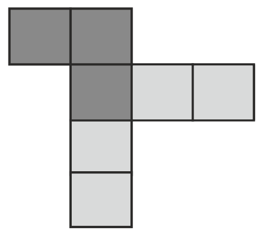
Add one blue square to the pattern to make a new pattern that has a line of symmetry. Draw the line of symmetry of the new pattern. Describe the line of symmetry; that is, the line is a vertical, horizontal or diagonal line of symmetry.
Sofia has made this pattern from yellow and blue tiles. She also has two spare blue tiles.
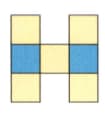
There are eight different ways I can add the two blue tiles to the pattern to make a pattern with one line of symmetry.
There are two different ways I can add the two blue tiles to the pattern to make a pattern with two lines of symmetry.
There is only one way I can add the two blue tiles to the pattern to make a pattern with four lines of symmetry.
Show that Sofia's statement are correct. You may join the tiles either side to side  or corner to corner
or corner to corner  .
.
Song has five blue tiles and four white tiles.

Draw two different ways that Song could arrange these tiles so that he has a shape with an order of rotational symmetry of .
Song has five blue tiles and four white tiles.

Draw two different ways that Song could arrange these tiles so that he has a shape with an order of rotational symmetry of . For each of the patterns you drew, how many lines of symmetry do your patterns of tiles have.
