M L Aggarwal Solutions for Chapter: Probability, Exercise 1: Exercise 15
M L Aggarwal Mathematics Solutions for Exercise - M L Aggarwal Solutions for Chapter: Probability, Exercise 1: Exercise 15
Attempt the practice questions on Chapter 15: Probability, Exercise 1: Exercise 15 with hints and solutions to strengthen your understanding. CBSE Syllabus Standard Mathematics for Class IX solutions are prepared by Experienced Embibe Experts.
Questions from M L Aggarwal Solutions for Chapter: Probability, Exercise 1: Exercise 15 with Hints & Solutions
The distance (in ) of engineers from their residence to their place of work is found as follows:
What is the empirical probability that an engineer lives less than from his/her place of work?
The distance (in ) of engineers from their residence to their place of work is found as follows:
What is the empirical probability that an engineer lives more than or equal to from his/her place of work?The distance (in ) of engineers from their residence to their place of work is found as follows:
What is the empirical probability that an engineer lives within from his/her place of work?A company selected households at random and surveyed them to find out a relationship between income level and the number of television sets in a home, The information so obtained is listed in the following table:
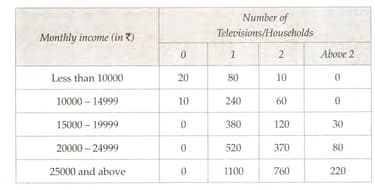
A company selected households at random and surveyed them to find out a relationship between income level and the number of television sets in a home, The information so obtained is listed in the following table:
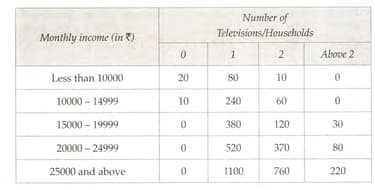
A company selected households at random and surveyed them to find out a relationship between income level and the number of television sets in a home, The information so obtained is listed in the following table:
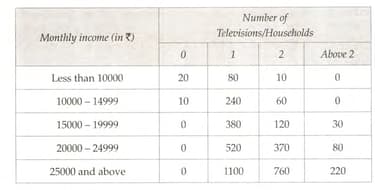
Two sections of class of a school having students in each section appeared for mathematics olympiad. The marks obtained by them are given below:
One student is selected at random. Find the probability that selected student is having marks more than .
Two sections of class of a school having students in each section appeared for mathematics olympiad. The marks obtained by them are given below:
One student is selected at random. Find the probability that selected student is having marks between and .
