M L Aggarwal Solutions for Chapter: Surface Areas and Volumes, Exercise 9: Chapter Test

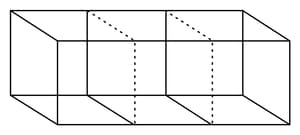
Three cubes, each of side $6 \mathrm{cm}$ are joined side-by-side (as shown in the figure below) to form a cuboid. Find the volume and the surface area of the cuboid.

If three cubes of metal whose edges are in the ratio $3:4:5$ are melted and recasted into a single cube of diagonal $12\sqrt{3} \mathrm{cm}$, then find the edges of the three cubes.

A cylinder of maximum volume is cut out from a wooden cuboid of length $30 \mathrm{cm}$ and cross-section a square of side $14 \mathrm{cm}$. Find the volume of the cylinder and the volume of wood wasted. Take $\mathrm{\pi }=\frac{22}{7}$.

The sum of the radius and height of a cylinder is $37 \mathrm{cm}$ and the total surface area of the cylinder is $1628{ \mathrm{cm}}^2$. Find the height and the volume of the cylinder. Take $\mathrm{\pi }=\frac{22}{7}$.

Find the volume and the total surface area of a cone having slant height $17 \mathrm{cm}$ and base diameter $30 \mathrm{cm}$. Take $\pi =3.14$.

The radius and the height of a right circular cone are in the ratio $5:12$. If its volume is $314{ \mathrm{cm}}^3$, find its slant height and the curved surface area (use $\pi =3.14$).

Find what length of canvas $2 \mathrm{m}$ in width is required to make a conical tent $20 \mathrm{m}$ in diameter and $42 \mathrm{m}$ in slant height allowing $10\%$ for folds and stitching. Also, find the cost of canvas at the rate of $₹80$ per metre.

If the volume of a sphere is $179\frac{2}{3} {\mathrm{cm}}^3$, find its radius and surface area.