M L Aggarwal Solutions for Chapter: Appendix Mathematical Modelling, Exercise 9: TRIGONOMETRY

From the top of a $75 \mathrm{m}$ high lighthouse, a person observes two ships due East.

What is the distance of the ship $\mathrm{B}$ from the lighthouse?

From the top of a $75 \mathrm{m}$ high lighthouse, a person observes two ships due East.

What is the distance between the ships?

From the top of a $75 \mathrm{m}$ high lighthouse, a person observes two ships due East.

To warn ships about the underwater rocks, the lighthouse spreads a Red coloured light over a sector of angle $120°$ to a distance of $21 \mathrm{km}$. How much of the area of the sea in $\mathrm{sq}.\mathrm{km}$ is warned by the red light from the lighthouse.

The angle of elevation of the top of a tower from the top of a $7 \mathrm{m}$ tall building is $60°$ and the angle of depression of the foot $\mathrm{C}$ of the tower from the same point is found to be $45°$.

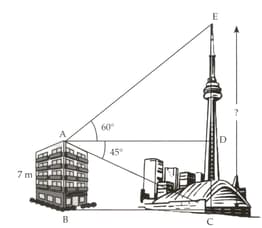
The distance between the tower and the building is 

The angle of elevation of the top of a tower from the top of a $7 \mathrm{m}$ tall building is $60°$ and the angle of depression of the foot $\mathrm{C}$ of the tower from the same point is found to be $45°$.

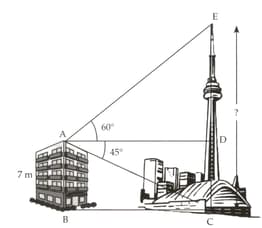
How much is the distance $\mathrm{AC}$?

The angle of elevation of the top of a tower from the top of a $7 \mathrm{m}$ tall building is $60°$ and the angle of depression of the foot $\mathrm{C}$ of the tower from the same point is found to be $45°$.

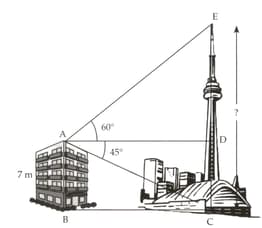
What is the height of the tower?

The angle of elevation of the top of a tower from the top of a $7 \mathrm{m}$ tall building is $60°$ and the angle of depression of the foot $\mathrm{C}$ of the tower from the same point is found to be $45°$.

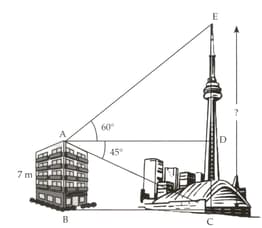
If the angle of depression of the foot of the tower from the top of the building is $60°$, the height of the tower will be 

A $120 \mathrm{m}$ tall tower throws a shadow $90 \mathrm{m}$ long at a particular time, what will be the length of the shadow of a $40 \mathrm{m}$ tall building?