M L Aggarwal Solutions for Chapter: Areas Related to Circles, Exercise 7: Chapter Test

A cube whose each edge is $28 \mathrm{cm}$ long has a circle of maximum radius on each of its face painted red. Find the total area of the unpainted surface of the cube.

On a square cardboard sheet of area $784 {\mathrm{cm}}^2$, four congruent circular plates of maximum size are placed such that each circular plate touch the other two plates and each side of the square sheet is tangent to two circular plates. Find the area of the square sheet not covered by circular plates.

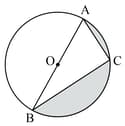
In the figure, $\mathrm{O}$ is the centre of the circle. If $\mathrm{BC}=24 \mathrm{cm}$ and $\mathrm{AC}=10 \mathrm{cm}$, find the area of the shaded region. (Use $\mathrm{\pi }=3.14$)

A wire bent in the form of a circle of radius $42 \mathrm{cm}$ is cut and again bent in the form of a square. Find the ratio of the areas of the regions enclosed by the circle and the square.

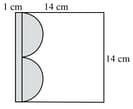
In the figure, from a sheet of cardboard in the shape of a square of side $14 \mathrm{cm}$, a piece in the shape of the letter $\mathbf{B}$ is cut off. The curved side of the letter consists of two equal semicircles and the breadth of the rectangular piece is $1 \mathrm{cm}$. Find the area of the remaining part of the cardboard.

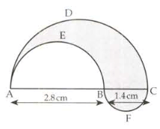
In the figure, $\mathrm{ADC}, \mathrm{AEB}$ and $\mathrm{BFC}$ are semicircles on diameters $\mathrm{AC}, \mathrm{AB}$ and $\mathrm{BC}$ respectively. Find the perimeter of the shaded region.

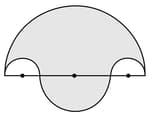
In the figure, the boundary of the shaded region consists of four semicircular arcs, the smallest two being equal. If the diameter of the largest is $14 \mathrm{cm}$ and of the smallest is $3.5 \mathrm{cm}$, calculate the length of the boundary.

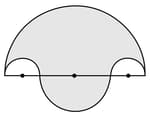
In the figure, the boundary of the shaded region consists of four semicircular arcs, the smallest two being equal. If the diameter of the largest is $14 \mathrm{cm}$ and of the smallest is $3.5 \mathrm{cm}$. Calculate the area of the shaded region.