M L Aggarwal Solutions for Chapter: Heights and Distances, Exercise 1: Exercise 12

The angle of elevation of the top of a vertical tower from a point on the ground is $60°$. From another point $10 m$ vertically above the first point, its angle of elevation is $30°$. Find the height of the tower.

From the base of a $30 m$ high building, the angle of elevation of a tower is $60°$, and from the top of the building it is $30°$. Find the height of the tower and the distance between the building and the tower.

There are two poles, one each on either bank of a river just opposite to each other. One of the pole is $60 m$ high. From the top of this pole, the angles of depression of the top and foot of the other pole are $30°$ and $60°$ respectively. Find the width of the river and the height of the other pole.

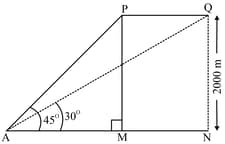
The angle of elevation of the top $Q$ of a vertical tower $PQ$ from a point $X$ on the ground is $60°$. From a point $Y, 40 m$ vertically above $X$, the angle of elevation of the top $Q$ of the tower is $45°$.Find the height of the tower $PQ$ and the distance $PX$. (Use $\sqrt{3}=1.73$)

A man standing on the deck of a ship, which is $10 m$ above water level, observes the angle of elevation of the top of a hill as $60°$ and angle of depression of the base of the hill as $30°$. Find the difference of the hill from the ship and the height of the hill.

The angle of elevation of a cloud from a point $60 m$ above a lake is $30°$ and the angle of depression of its reflection in the lake is $60°$. Find the height of the cloud.

The angle of elevation of an aeroplane from a point $A$ on the ground is $60°$. After a flight of $30 seconds$, the angle of elevation changes to $30°$. If the aeroplane is flying at a constant height of $3000\sqrt{3} m$, find the speed of the aeroplane in $km/h$.

In the below given figure, the angle of elevation of a helicopter from a point $A$ on the ground is $45°$. After $15 seconds$ flight, the angle of elevation changes to $30°$. If the helicopter is flying at a height of $2000 m$, find the speed of the helicopter. Take $\sqrt{3}=1.732$