M L Aggarwal Solutions for Chapter: Surface Areas and Volumes, Exercise 4: Exercise 14.4

A cone is of height $24 cm$ and the base radius $9 cm.$ Find the radius of the circular section cut from the cone by a plane parallel to the base and $8 cm$ from it.

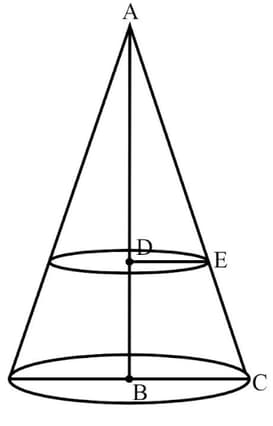
The perimeters of the ends of a frustum of a (solid) cone are $36 cm$ and $48 cm$ . If the height of the frustum is $11 cm ,$ , find its volume.

The diameter of the lower and upper ends of a bucket (in the form of a frustum of a cone) are $10 cm$ and $30 cm$ Respectively . If its height is $24 cm$, find the capacity of the bucket.

The diameter of the lower and upper ends of a bucket in the form of a frustum of a cone are $10\mathrm{cm}$ and $30\mathrm{cm}$ respectively. If its height is $24\mathrm{cm},$ find the area of the metal sheet used to make the bucket.  [Use $\pi =3.14]$

The radii of the ends of a frustum of a cone $45 cm$ 45 cm high are $28 cm$ 28 cm  and $7 cm.$ 7 cm Find its volume, curved surface area and the total surface area.

A container open at the top, is in the form of a frustum of a cone of height 24cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of $₹21$ per litre.

A container open at the top and made up of metal sheet is in the form of a frustum of a cone of height 16cm with diameters of its lower and upper ends as $16 cm$ and $40 cm$ respectively . Find the cost of metal sheet to make the container , if it costs $₹10$ per $100 c{m}^2$. $($Use $\pi =3.14)$

The height of a cone is $30 cm$. A small cone is cut off at the top by a plane parallel to its base. If its volume be $\frac{1}{27}$ of the volume of the given cone, at what height above the base is the section cut?