M L Aggarwal Solutions for Exercise 2: Exercise 20

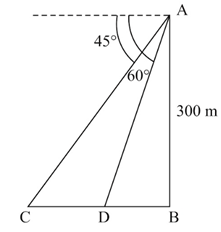
In the adjoining figure, not drawn to the scale, $AB$ is a tower and two objects $C$ and $D$ are located on the ground, on the same side of $AB$. When observed from the top $A$ of the tower, their angles of depression are $45°$ and $60°$. Find the distance between the two objects, if the height of the tower is $300 \mathrm{m}$. Give your answer to the nearest metre.

The horizontal distance between two towers is $140 \mathrm{m}$. The angle of elevation of the top of the first tower, when seen from the top of the second tower is $30°$. If the height of the second tower is $60 \mathrm{m}$, find the height of the first tower.

From a tower $126 \mathrm{m}$ high, the angles of depression of two rocks which are in a horizontal line through the base of the tower are $16°$ and $12° 20°$. Find the distance between the rocks if they are on

(i) the same side of the tower

(ii) the opposite sides of the tower.

A man $1.8 \mathrm{m}$ high stands at a distance of $3.6 \mathrm{m}$ from a lamp post and casts a shadow of $5.4 \mathrm{m}$ on the ground. Find the height of the lamp post.

The angles of depression of the top and the bottom of a $8 \mathrm{m}$ tall building from the top of a multi-storeyed building are $30°$ and $45°$ respectively. Find the height of the multi-storeyed building and the distance between the two buildings, correct to two decimal places.

A pole of height $5 \mathrm{m}$ is fixed on the top of a tower. The angle of elevation of the top of the pole as observed from a point $A$ on the ground is $60°$ and the angle of depression of the point A from the top of the tower is $45°$. Find the height of the tower. (Take $\sqrt{3}=1.732$)

A vertical pole and a vertical tower are on the same level ground. From the top of the pole, the angle of elevation of the top of the tower is $60°$ and the angle of depression of the foot of the tower is $30°$. Find the height of the tower if the height of the pole is $20 \mathrm{m}$.

From the top of a building $20 \mathrm{m}$ high, the angle of elevation of the top of a monument is $45°$ and the angle of depression of its foot is $15°$. Find the height of the monument.