Distance Formula

Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.

$\mathrm{A}=\left(-3,5\right),\mathrm{B}=\left(3,1\right),\mathrm{C}=\left(0,3\right),\mathrm{D}=\left(-1,-4\right)$

Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:

$\left(4,\mathrm{}5\right),\mathrm{}\left(7,\mathrm{}6\right),\mathrm{}\left(4,\mathrm{}3\right),\mathrm{}\left(1,\mathrm{}2\right)$

Find the distance between the following pair of points.

$\left(-5,7\right), \left(-1,3\right)$

Find the distance between the pair of points: $\left(\mathrm{a},\mathrm{b}\right),\left(-\mathrm{a},-\mathrm{b}\right)$

$\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ is a rectangle formed by the points $\mathrm{}\mathrm{A}\left(-1,\mathrm{}-1\right),\mathrm{}\mathrm{B}\left(-1,\mathrm{}4\right),\mathrm{}\mathrm{C}\left(5,\mathrm{}4\right)$and $\mathrm{}\mathrm{D}\left(5,\mathrm{}-1\right)$. $\mathrm{}\mathrm{P},\mathrm{}\mathrm{Q},\mathrm{}\mathrm{R}$ and $\mathrm{}\mathrm{S}$ are the midpoints of $\mathrm{}\mathrm{A}\mathrm{B},\mathrm{}\mathrm{B}\mathrm{C},\mathrm{}\mathrm{C}\mathrm{D}$ and $\mathrm{}\mathrm{D}\mathrm{A}$ respectively. Is the quadrilateral $\mathrm{}\mathrm{P}\mathrm{Q}\mathrm{R}\mathrm{S}$ a square? A rectangle? Or a rhombus? Justify your answer.

The two opposite vertices of a square are $\left(-1,\mathrm{}2\right)$ and $\left(3,\mathrm{}2\right)$. Find the coordinates of the other two vertices.

Find the centre of a circle passing through the points $\left(6,\mathrm{}-6\right),\mathrm{}\left(3,\mathrm{}-7\right)$ and $\left(3,\mathrm{}3\right)$.

Find a relation between $x$ and $y$ such that the point $\left(x,\mathrm{}y\right)$ is equidistant from the point $\left(3,\mathrm{}6\right)$ and $\left(-3,\mathrm{}4\right)$.

If $\mathrm{}\mathrm{Q}\left(0,\mathrm{}1\right)$ is equidistant from $\mathrm{}\mathrm{P}\left(5,\mathrm{}-3\right)$ and $\mathrm{}\mathrm{R}\left(x,\mathrm{}6\right)$, find the values of $x$. Also find the distances $\mathrm{}\mathrm{Q}\mathrm{R}$ and $\mathrm{}\mathrm{P}\mathrm{R}$.

Find the values of $y$ for which the distance between the points $\mathrm{}\mathrm{P}\left(2,\mathrm{}-3\right)$ and $\mathrm{}\mathrm{Q}(10,\mathrm{}y)$ is $\mathrm{}10\mathrm{}$ units.

Find the point on the $x-$axis which is equidistant from $\left(2,\mathrm{}-5\right)$ and $\left(-2,\mathrm{}9\right)$.

Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
 $\left(-1,\mathrm{}-2\right),\mathrm{}\left(1,\mathrm{}0\right),\mathrm{}\left(-1,\mathrm{}2\right),\mathrm{}\left(-3,\mathrm{}0\right)$
 

In a classroom, $\mathrm{}4$ friends are seated at the points $\mathrm{}\mathrm{A},\mathrm{}\mathrm{B},\mathrm{}\mathrm{C}$ and $\mathrm{}\mathrm{D}$ as shown in Fig. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think $\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ is a square?” Chameli disagrees.

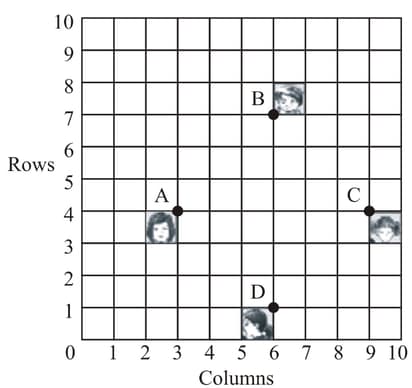
Using distance formula, find which of them is correct.

Check whether $\left(5,\mathrm{}-2\right),\mathrm{}\left(6,\mathrm{}4\right)$ and $\left(7,\mathrm{}-2\right)$ are the vertices of an isosceles triangle.

Determine if the points $\left(1,\mathrm{}5\right),\mathrm{}\left(2,\mathrm{}3\right)$ and $\left(-2,\mathrm{}-11\right)$ are collinear.

Find the distance between the points $\left(0,\mathrm{}0\right)$ and $\left(36,\mathrm{}15\right)$.

Find the distance between the following pairs of points:
$\left(2,3\right),\left(4,1\right)$