Heights and Distances

The angles of elevation of the top of a tower from two points at a distance of $4 \mathrm{m}$ and $9 \mathrm{m}$ from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is $6 \mathrm{m}$.

A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of $\mathrm{}{30}^{\mathrm{o}}$, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be $\mathrm{}{60}^{\mathrm{o}}$.

Find the time taken by the car to reach the foot of the tower from this point.

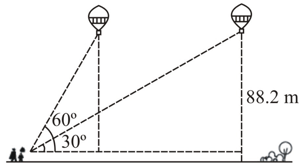
A $1.2 \mathrm{m}$ tall girl spots a balloon moving with the wind in a horizontal line at a height of $88.2 \mathrm{m}$ from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is $60°$. After some time, the angle of elevation reduces to $30°$ (see Fig.). Find the distance travelled by the balloon during the interval.

As observed from the top of a $75 \mathrm{m}$ high lighthouse from the sea-level, the angles of depression of two ships are $30°$ and $45°$. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.

From the top of a $7 \mathrm{m}$ high building, the angle of elevation of the top of a cable tower is $60°$ and the angle of depression of its foot is $45°$. Determine the height of the tower.

A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is $60°$. From another point $20 \mathrm{m}$ away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is $30°$. Find the height of the tower and the width of the canal.

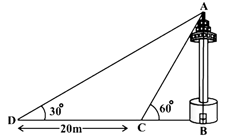
Two poles of equal heights are standing opposite each other on either side of the road, which is $80 \mathrm{m}$ wide. From a point between them on the road, the angles of elevation of the top of the poles are $60°$ and $30°$, respectively. Find the height of the poles and the distances of the point from the poles.

The angle of elevation of the top of a building from the foot of the tower is $\mathrm{}{30}^{\mathrm{o}}$ and the angle of elevation of the top of the tower from the foot of the building is $60°$. If the tower is $50 \mathrm{m}$ high, find the height of the building.

A statue $1.6 \mathrm{m}$ tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is $60°$ and from the same point the angle of elevation of the top of the pedestal is $45°$. Find the height of the pedestal.

From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a $20 \mathrm{m}$ high building are $45°$ and $60°$ respectively. Find the height of the tower.

A $1.5 \mathrm{m}$ tall boy is standing at some distance from a $30 \mathrm{m}$ tall building. The angle of elevation from his eyes to the top of the building increases from $30°$ to $60°$ as he walks towards the building. Find the distance he walked towards the building.

A kite is flying at a height of $60 \mathrm{m}$ above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is $60°$. Find the length of the string, assuming that there is no slack in the string.

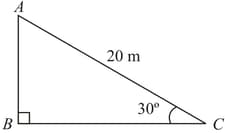
The angle of elevation of the top of a tower from a point on the ground, which is $30 \mathrm{m}$ away from the foot of the tower is $30°$. Find the height of the tower.

A contractor plans to install two slides for the children to play in a park. For the children below the age of $5$ years, she prefers to have a slide whose top is at a height of $1.5 \mathrm{m}$, and is inclined at an angle of $30°$ to the ground, whereas for elder children, she wants to have a steep slide at a height of $3 \mathrm{m}$, and inclined at an angle of $60°$ to the ground. What should be the length of the slide in each case ?

A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle $30°$ with it. The distance between the foot of the tree to the point where the top touches the ground is $8 \mathrm{m}$. Find the height of the tree.

A circus artist is climbing a $20 \mathrm{m}$ long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is $30°$ (see figure).