Assam Board Solutions for Chapter: Surface Areas and Volumes, Exercise 1: Exercise 13.1
Assam Board Mathematics Solutions for Exercise - Assam Board Solutions for Chapter: Surface Areas and Volumes, Exercise 1: Exercise 13.1
Attempt the practice questions on Chapter 13: Surface Areas and Volumes, Exercise 1: Exercise 13.1 with hints and solutions to strengthen your understanding. MATHEMATICS Textbook for Class X solutions are prepared by Experienced Embibe Experts.
Questions from Assam Board Solutions for Chapter: Surface Areas and Volumes, Exercise 1: Exercise 13.1 with Hints & Solutions
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is and the total height of the vessel is . Find the inner surface area of the vessel.
A toy is in the form of a cone of radius mounted on a hemisphere of same radius. The total height of the toy is . Find the total surface area of the toy.
A cubical block of side is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
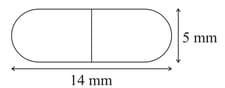
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig.). The length of the entire capsule is and the diameter of the capsule is . Find its surface area.
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are and respectively, and the slant height of the top is , find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of . (Note that the base of the tent will not be covered with canvas.)
From a solid cylinder whose height is and diameter , a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest .
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is , and its base is of radius , find the total surface area of the article.