Assam Board Solutions for Chapter: Triangles, Exercise 4: Exercise 6.4

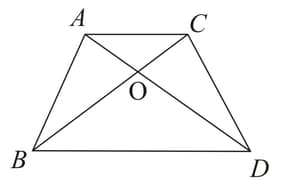
Diagonals of a trapezium $\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ with $\mathrm{}\mathrm{A}\mathrm{B}\parallel \mathrm{D}\mathrm{C}$ intersect each other at the point $\mathrm{}\mathrm{O}$. If $\mathrm{}\mathrm{A}\mathrm{B}=2\mathrm{C}\mathrm{D}$, find the ratio of the areas of triangles $\mathrm{}\mathrm{A}\mathrm{O}\mathrm{B}$ and $\mathrm{}\mathrm{C}\mathrm{O}\mathrm{D}$.

In the figure,  $\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}$ and $\mathrm{}\mathrm{D}\mathrm{B}\mathrm{C}$ are two triangles on the same base $\mathrm{}\mathrm{B}\mathrm{C}$. If $\mathrm{}\mathrm{A}\mathrm{D}$ intersects $\mathrm{}\mathrm{B}\mathrm{C}$ at $\mathrm{}\mathrm{O}$, show that $\frac{\mathrm{a}\mathrm{r}\mathrm{}\left(\mathrm{A}\mathrm{B}\mathrm{C}\right)}{\mathrm{a}\mathrm{r}\mathrm{}\left(\mathrm{D}\mathrm{B}\mathrm{C}\right)}=\frac{\mathrm{A}\mathrm{O}}{\mathrm{D}\mathrm{O}}$.

If the areas of two similar triangles are equal, prove that they are congruent.

$\mathrm{D}, \mathrm{E}$ and $\mathrm{}\mathrm{F}$ are respectively the mid-points of sides $\mathrm{A}\mathrm{B}, \mathrm{B}\mathrm{C}$ and $\mathrm{}\mathrm{C}\mathrm{A}$ of $\mathrm{}∆\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}$. Find the ratio of the areas of $\mathrm{}∆\mathrm{}\mathrm{D}\mathrm{E}\mathrm{F}$ and $\mathrm{}∆\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}$.

Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.

$\mathrm{A}\mathrm{B}\mathrm{C}$ and $\mathrm{}\mathrm{B}\mathrm{D}\mathrm{E}$ are two equilateral triangles such that $\mathrm{}\mathrm{D}$ is the midpoint of $\mathrm{}\mathrm{B}\mathrm{C}$. Ratio of the areas of triangles $\mathrm{}\mathrm{A}\mathrm{B}\mathrm{C}$ and $\mathrm{}\mathrm{B}\mathrm{D}\mathrm{E}$ is

Sides of two similar triangles are in the ratio $\mathrm{}4\mathrm{}:9$. Areas of these triangles are in the ratio