Umakant Kondapure, Collin Fernandes, Nipun Bhatia, Vikram Bathula and, Ketki Deshpande Solutions for Chapter: Rotational Motion, Exercise 2: Critical Thinking

A disc of uniform thickness and radius $50 \mathrm{cm}$ is made of two zones. The central zone of radius $20.0 \mathrm{cm}$ is made of metal and has a mass of $4.00 \mathrm{kg}$. The outer zone is of wood and has a mass of $3.00 \mathrm{kg}$. The M.I. of the disc about a transverse axis through its centre is, 

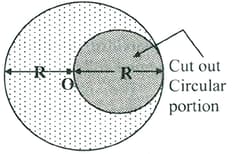
A circular portion of diameter $R$ is cut out from a uniform circular disc of mass $M$ and radius $R$ as shown in the figure. The moment of inertia of the remaining (shaded) portion of the disc about an axis passing through the centre $O$ of the disc and perpendicular to its plane is,

A wheel is rotating freely at an angular speed of $800 \mathrm{rev} {\min }^{-1}$ On a shaft whose rotational inertia is negligible. A second wheel initially at rest with thrice the rotational inertia of the first is suddenly coupled to the same shaft. The fraction of original kinetic energy lost is,
 

A wheel rotates with angular velocity $500 \mathrm{rpm}$ On a shaft. Second identical wheel axially at rest is suddenly coupled on same shaft. What is the total angular speed of the system? [Assume M.I. of shaft to be negligible.]

If the radius of the earth contracts to half of its present value keeping mass constant, then the length of the day will be,

Two discs of moments of inertia $I_1$ and $I_2$ About their respective axes, rotating with angular frequencies ${\omega }_1$ and ${\omega }_2$, respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be,

A pot maker rotates pot making wheel of radius $3 \mathrm{m}$ By applying a force of $200 \mathrm{N}$ Tangentially. Because of this, the wheel completes exactly $1\frac{1}{2}$ Revolution. The work done by him is,

Assertion: A solid cylinder of mass $m$ and radius $R$ rolls down an inclined plane of height
$H$. The rotational kinetic energy of the cylinder when it reaches the bottom of the plane is $\frac{mgH}{3}$.

Reason: The total energy of the cylinder remains constant throughout its motion.