Analytical Treatment of Interference Bands

A thin plastic sheet of refractive index $1.6$ is used to cover one of the slits of a double-slit arrangement. The central point on the screen is now occupied by what would have been the $7$ bright fringe before the plastic was used. If the wavelength of light is $600 \mathrm{nm}$, what is the thickness (in $\mu \mathrm{m}$) of the plastic? 

A thin mica sheet of thickness $2\times {10}^{-6} \mathrm{m}$ and refractive index $(\mu =1.5)$ is introduced in the path of the first wave. The wavelength of the wave used is $5000 \stackrel{\circ }{\mathrm{A}}$. The central bright maximum will shift

Two interfering waves are arriving at a point on a screen with a path difference of $120\lambda$. The path difference is $72$$\mu m$. The wavelength of light is _____. Is the point dark or bright? 

The optical path difference between the two identical waves arriving at a point is $0.05 \mathrm{cm}$. If the wavelength of light used is $5000 \stackrel{\circ }{\mathrm{A}}$, then the number of dark fringes passing through that point will be

In Young's double-slit experiment, two wavelengths ${\lambda }_1=780 \mathrm{nm}$ and ${\lambda }_2=520 \mathrm{nm}$ are used to obtain interference fringes. If the $n^{\mathrm{th}}$ bright band due to ${\lambda }_1$ coincides with $(n+1{)}^{\mathrm{th}}$ bright band due to ${\lambda }_2$, then the value of $n$ is 

In Young's double-slit experiment, the slits are $2 \mathrm{mm}$ apart and are illuminated by photons of two wavelengths ${\lambda }_1=12000 \stackrel{\circ }{\mathrm{A}}$ and ${\lambda }_1=10000 \stackrel{\circ }{\mathrm{A}}$. At what minimum distance from the common central bright fringe on the screen $2 \mathrm{m}$ from the slit will a bright fringe from one interference pattern coincide with a bright fringe from the other? 

In Young's double-slit experiment, slits are separated by $0.5 \mathrm{mm}$ and the screen is placed $150 \mathrm{cm}$ away. A beam of light consisting of two wavelengths $650 \mathrm{nm}$ and $520 \mathrm{nm}$, is used to obtain interference fringes on the screen. The least distance from the bright fringes due to both the wavelengths coincide is

The two slits are $1 \mathrm{mm}$ apart from each other and illuminated with a light of wavelength $5\times {10}^{-7} \mathrm{m}$. If the distance of the screen is $1 \mathrm{m}$ from the slits, then the distance between the third dark fringe and the fifth bright fringe is

In the double-slit experiment, the angular width of the fringes is $0.20°$ for the sodium light $(\lambda =5890 \stackrel{\circ }{\mathrm{A}})$. In order to increase the angular width of the fringes by $10 \%$, the necessary change in the wavelength is 

In Young's experiment, two coherent sources are placed $0.90 \mathrm{mm}$ apart and the fringes are observed one metre away. If it produces the second dark fringe at a distance of $1 \mathrm{mm}$ from the central fringe, the wavelength of monochromatic light used would be

The maximum intensity in Young's double slit experiment is $I_0.$ Distance between the slits is $\mathrm{d}=2\lambda ,$ where $\lambda$ is the wavelength of monochromatic light used in experiment. What will be the intensity of light in front of one of the slits on a screen at a distance $D=6 d$ ?

In a Young's double slit experimental arrangement shown here, if a mica sheet of thickness $t$ and refractive index $\mu$ is placed in front of the slit $\mathrm{S}_{1},$ then the path difference $\left({\mathrm{S}}_1\mathrm{P}-{\mathrm{S}}_2\mathrm{P}\right)$

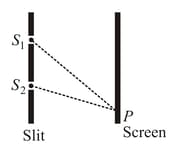
In Young's double-slit experiment, an interference pattern is obtained on a screen by a light of wavelength $6000 \mathrm{\AA }$ coming from the coherent sources $\mathrm{S}_{1}$ and $\mathrm{S}_{2}$. At certain point $P$ on the screen, third dark fringe is formed. Then the path difference $S_{1} P-S_{2} P$ in microns is

Two slits separated by a distance of $1 \mathrm{mm}$ are illuminated with red light of wavelength $6.5\times {10}^{-7} \mathrm{m}$. The interference fringes are observed on a screen placed $1 \mathrm{m}$ from the slits. The distance between third bright fringe and the fifth dark fringe on the same side is equal to

In the double-slit experiment, the distance of the second dark fringe from the central line is $3 \mathrm{mm}$. The distance of the fourth bright fringe from the central line is

Two sources of light $0.5 \mathrm{mm}$ apart are placed at a distance of $1.2 \mathrm{m}$ and wavelength of light is $5000 \mathrm{\AA }$. The phase difference between the two light waves interfering on the screen at a point at a distance $3 \mathrm{mm}$ from central bright band is

Two wavelengths of light ${\lambda }_1$ and ${\lambda }_2$ are sent through Young's double slit apparatus simultaneously. If $3^{rd}$ order bright fringe of ${\lambda }_1$ coincide with the fourth order bright fringe for ${\lambda }_2,$ then $\frac{{\lambda }_1}{{\lambda }_2}=$

If a thin transparent plate is introduced in the path of interfering waves, then entire fringe

The distance of $n^{\text {th }}$ bright band from centre band is given by,

In interference of light, bright bands occur on the screen at