Rose Harrison and Clara Huizink Solutions for Exercise 19: Mixed practice

The graph shows the motion of a tall building as it sways to and fro in the wind.

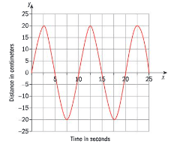
Determine the period, and explain what it means in this problem.

The graph shows the motion of a tall building as it sways to and fro in the wind.

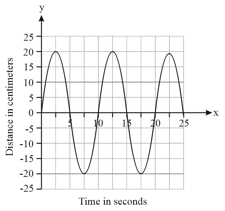
State the maximum number of centimetres that the tall building sways from its vertical position.

The graph shows the motion of a tall building as it sways to and fro in the wind.

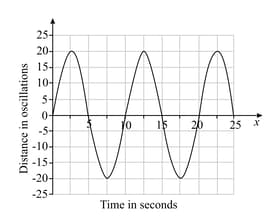
Find a sinusoidal function to model this situation.

A nail is stuck in a car tyre. The height of the nail above the ground varies as the wheel turns and can be modelled by this graph.

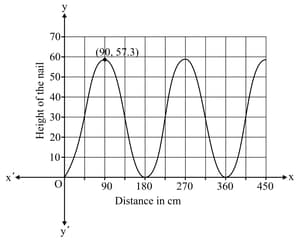
Find the period of the graph, and explain what it means in this situation.

A nail is stuck in a car tyre. The height of the nail above the ground varies as the wheel turns and can be modelled by this graph.

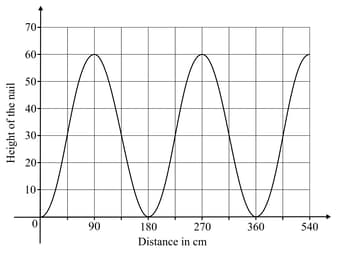
The radius of the wheel is $a cm$. Find the value of $a.$

When the sun first rises, the angle of elevation increases rapidly at first, then more slowly, until the maximum angle is reached at about noon. The angle then decreases until sunset.

Assume that the relationship between the time of the day and the angle of elevation is sinusoidal.

Let $t$ be the number of hours since midnight.

Let the amplitude be $60$ degrees.

The maximum angle of elevation occurs at noon.

The period is $24$ hours.

The angle of elevation at midnight is $-65$ degrees.

Explain the significance of the $t-$ intercepts.

When the sun first rises, the angle of elevation increases rapidly at first, then more slowly, until the maximum angle is reached at about noon. The angle then decreases until sunset.

Assume that the relationship between the time of the day and the angle of elevation is sinusoidal.

Let $t$ be the number of hours since midnight.

Let the amplitude be $60$ degrees.

The maximum angle of elevation occurs at noon.

The period is $24$ hours.

The angle of elevation at midnight is $-65$ degrees.

Predict the angle of elevation in degrees at $9:00$ in the morning and $2:00$ in the afternoon.

When the sun first rises, the angle of elevation increases rapidly at first, then more slowly, until the maximum angle is reached at about noon. The angle then decreases until sunset.

Assume that the relationship between the time of the day and the angle of elevation is sinusoidal.

Let $t$ be the number of hours since midnight.

Let the amplitude be $60$ degrees.

The maximum angle of elevation occurs at noon.

The period is $24$ hours.

The angle of elevation at midnight is $-65$ degrees.

Predict the time of sunrise.