Manipur Board Solutions for Chapter: Circles, Exercise 1: EXERCISE 10

$ABCD$ is a cyclic quadrilateral in which $AC$ and $BD$ are its diagonals. If $\angle DBC=55°$ and $\angle BAC=45°$, find $\angle BCD$.

Prove that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic.

A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

In the adjoining figure, $\angle ABC=70°, \angle ACB=55°$. Find $\angle BDC$.

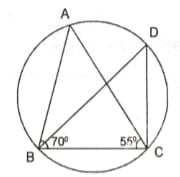
$ABCD$ is a cyclic quadrilateral whose diagonals intersect at a point $E$. If $\angle DBC=70°, \angle BAC= 30°$, find $\angle BCD$. Further, if $AB=BC$, find $\angle ECD$.

If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

In any triangle $ABC$, if angle bisector of $\angle A$ and perpendicular bisector of $BC$ intersect, prove that they intersect on the circumcircle of the triangle $ABC$.