Criteria for Similarity of Triangles
Important Questions on Criteria for Similarity of Triangles
Is the following pair of triangles similar? If so, find the similarity postulate used.
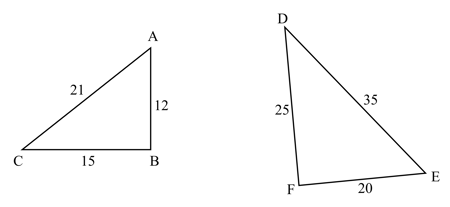
Is the following pair of triangles similar? If so, find the similarity postulate used.
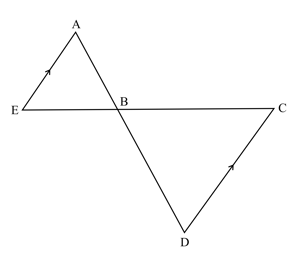
Is the following pair of triangles similar? If so, find the similarity postulate used.
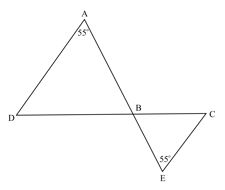
Is the following pair of triangles similar? If so, find the similarity postulate used.
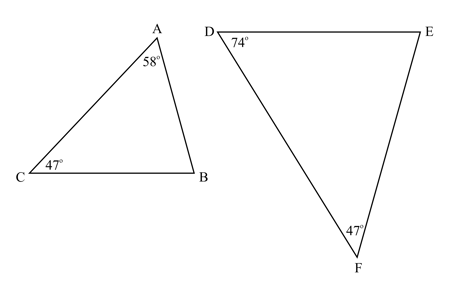
Write down the similarity postulate that proves the triangles are similar. Then find the missing measurement. Round your answers to 3 s.f.
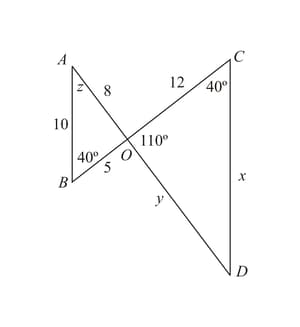
Write down the similarity postulate that proves the triangles are similar. Then find the missing measurement. Round your answers to 3 s.f.
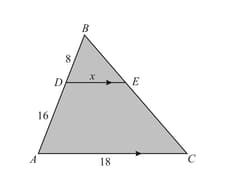
Prove that the line segment joining the midpoints of the sides of a triangle from four triangles, each of which is similar to the original triangle.
are respectively the medians of similar triangles and . Prove that .
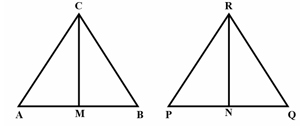
are respectively the medians of similar triangles and . Prove that .
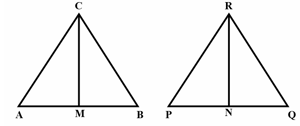
Are triangles formed in figure similar? If so, name the criterion of similarity. Write the similarity relation in symbolic form.
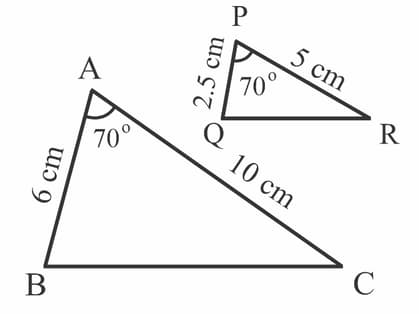
Are triangles formed in a figure similar? If so, name the criterion of similarity. Write the similarity relation in symbolic form.

In and . Prove that .
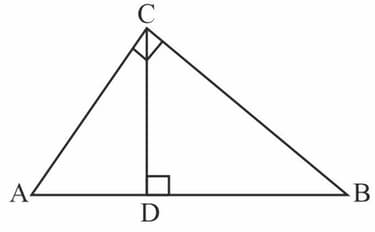
Is the pair of polygons given below similar or not similar? Why?
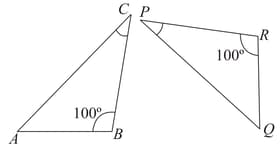
Check for similarity in the triangles and explain which criterion is used.
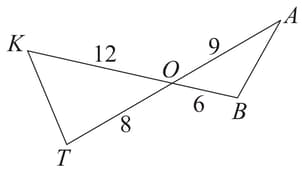
and
In the given figure, and . Prove that .
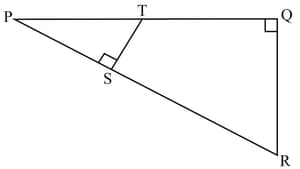
is the point of intersection of the diagonals and of a trapezium with . Through , a line segment is drawn parallel to meeting in and in , then is equal to
and are the points on sides and , respectively of . If , and , show that .
In the given figure, if and , prove that .
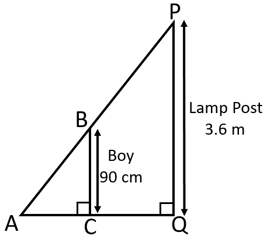
A boy of height is walking away from the base of a lamp-post at a speed of . If the lamp is above the ground, then the length of his shadow after is
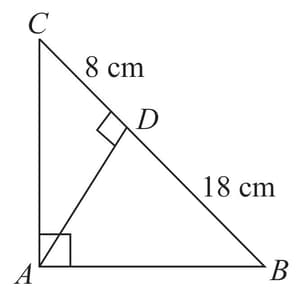
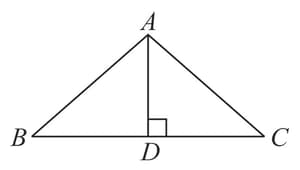
In the given figure, is a right-angled triangle with . is the perpendicular drawn on side dividing it into two parts. is and is . Prove that .