Section Formula
Important Questions on Section Formula
If the centroid of a triangle is at and two of its vertices are and , then find the third vertex of the triangle.
Find the centroid of the triangle whose veritices are and .
What are the coordinates of if point divides the line segment joining and internally in the ratio ?
In what ratio does the point divide the line segment joining the points and internally?
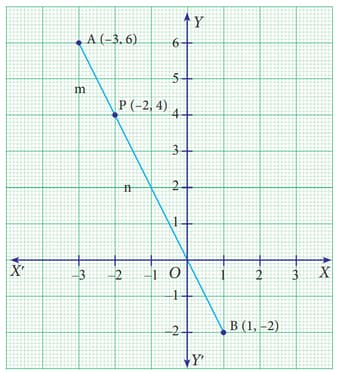
Find the coordinates of the point which divides the line segment joining the points and internally in the ratio .
Find the points of trisection of the line segment joining and .
The mid-points of the sides of a triangle are and . Find the coordinates of the vertices of the triangle.
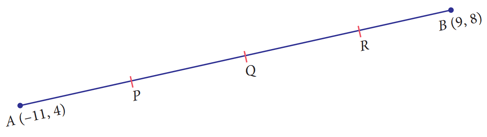
Find the points which divide the line segment joining and into four equal parts.
If and are the vertices of a parallelogram taken in order, then find the value of and .
The point is the centre of a circle. If is a diameter of the circle and is , find the coordinates of .
In what ratio does the axis divide the line joining the points and internally
If the coordinates of the midpoints of the sides and of a triangle are and respectively, then the vertices and of the triangle are
The ratio in which the axis divides the line segment joining the points and is
The ratio in which the axis divides the line segment joining the points and is
In what ratio does the point divides the line segment joining the points and ?
The coordinates of the point dividing the line segment joining the points and internally in the ratio is

