The Normal Distribution
Important Questions on The Normal Distribution
A random normal variable has mean and standard deviation . Given that . Find . [Use, ]
A random normal variable has mean and standard deviation . Given that . Find the value of . [Use, ]
A packing machine produces bags of rice whose weights are normally distributed with mean kg and standard deviation kg If a bag produced by this machine is selected at random, find the probability that its weight is more than kg given that it is less than kg. [Use, ]
A packing machine produces bags of rice whose weights are normally distributed with mean kg and standard deviation kg If a bag produced by this machine is selected at random, find the probability that its weight is between kg and kg.[Use, ]
A packing machine produces bags of rice whose weights are normally distributed with mean kg and standard deviation kg If a bag produced by this machine is selected at random, find the probability that its weight is less than kg. [Use, ]
A survey is conducted in a large factory. It is found that of the factory workers weigh less than kg and that of the factory workers weigh more than kg.
Assuming that the weights of the factory workers is modelled by a normal distribution with mean and standard deviation .
Find the probability that a factory worker chosen at random weighs more than kg.
A survey is conducted in a large factory. It is found that of the factory workers weigh less than kg and that of the factory workers weigh more than kg.
Assuming that the weights of the factory workers is modelled by a normal distribution with mean and standard deviation .
Determine two simultaneous linear equations satisfied by and .
Find the values of and .
An exam consists of true/false questions. John knows the correct answers to of the questions and decides to choose at random the answers to the remaining questions.
A student gains marks for each correct answer, has one mark subtracted for each incorrect answer, and gains no marks if the question is left unanswered.
Compare the expected number of marks when the student answers all the questions with the marks she will gain if she just answers the questions to which she knows the correct answer.
A survey is conducted in a large factory. It is found that of the factory workers weigh less than kg and that of the factory workers weigh more than kg.
Assuming that the weights of the factory workers is modelled by a normal distribution with mean and standard deviation .
Determine two simultaneous linear equations satisfied by and .
An exam consists of true/false questions. John knows the correct answers to of the questions and decides to choose at random the answers to the remaining questions.
Find the probability that John answers all the questions correctly.
An exam consists of true/false questions. John knows the correct answers to of the questions and decides to choose at random the answers to the remaining questions.
Find the probability that John answers questions correctly.
The factory has workers, of which are males. The weights of the males are normally distributed with mean and standard deviation .
If a male factory worker is selected at random, find the probability that he weights between and kilograms.
Find the expected number of male factory workers that weight more than kilograms.
The factory has workers, of which are males. The weights of the males are normally distributed with mean and standard deviation .
If a male factory worker is selected at random, find the probability that he weights between and kilograms.
Z is the standardised normal random variable with mean and variance . Find the value of such that .
The diagrams below each show a standard normal distribution. Find the values of
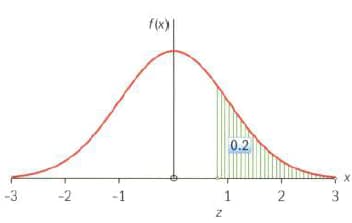
The diagrams below each show a standard normal distribution. Find the values of
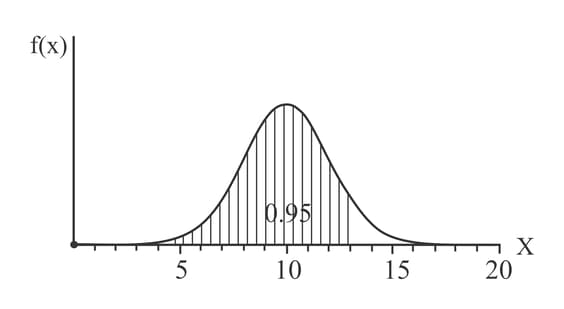
Find such that
Use the standard normal distribution
Find such that
Use the standard normal distribution
Find such that
Use the standard normal distribution

