Cyclic Quadrilateral

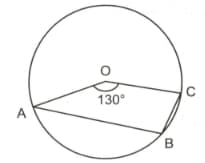
In the figure given below, $O$ is the centre of the circle such that $\angle AOC=130°$, then $\angle ABC=$

If $AB$ is a chord of a circle, $P$ and $Q$ are the two points on the circle different from $A$ and $B$, then

$PQRS$ is a cyclic quadrilateral such that $PR$ is a diameter of the circle. If $\angle QPR=67°$ and $\angle SPR=72°$, $\angle QRS=$

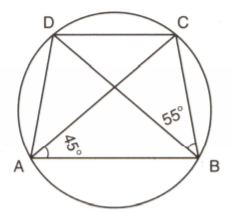
In the following figure, $ABCD$ is a cyclic quadrilateral in which $AC$ and $BD$ are its diagonals. If $\angle DBC=55°$, $\angle BAC=45°$ and $\angle BCD=k°$, then find the value of $k$.

$ABCD$ is a cyclic quadrilateral in which:

$\angle BCD=100°$ and $\angle ABD=70°$ find $\angle ADB$.

$ABCD$ is a cyclic quadrilateral in which $\angle DBC=80°$ and $\angle BAC=40°$. Find $\angle BCD$. 

$ABCD$ is a cyclic quadrilateral in which $BC \Vert AD,\angle ADC=110°$,  $\angle BAC=50°$ and $\angle DAC=k°$, then find the value of $k$.

In the following figure, $ABCD$ is a cyclic quadrilateral. Find the value of $x$.

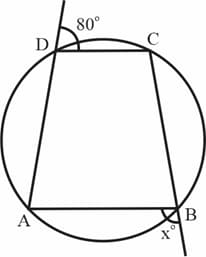
In the following figure, if $\angle BAC=60°$ and $\angle BCA=20°$ and $\angle ADC=k°$, then find the value of $k$.

.

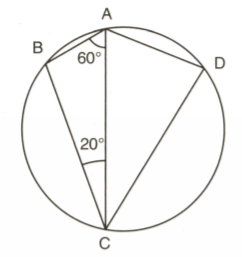
In a cyclic quadrilateral $ABCD$, if $m\angle A=3(m\angle C)$. Find $m\angle A$.

In the following figure, $AB$ and $CD$ are diameters of a circle with centre $O$ If $\angle OBD=50°$ find $\angle AOC$.

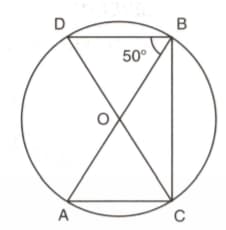
In the following figure, $O$ is the centre of the circle. Find $\angle CBD$.

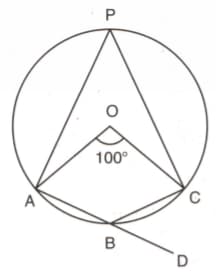
In the figure given below, $ABCD$ is a cyclic quadrilateral. If $\angle BCD=100°$ and $\angle ABD=70°,$ find $\angle ADB$.

Prove that the angle in a segment shorter than a semicircle is greater than a right angle.

$ABCD$ is a cyclic quadrilateral in which $BA$ and $CD$ when produced meet in $E$ and $EA=ED$ Prove that:

$EB=EC$

$ABCD$ is a cyclic quadrilateral in which $BA$ and $CD$ when produced meet in $E$ and $EA=ED$ Prove that:

$AD\Vert BC$

Prove that the centre of the circle circumscribing the cyclic rectangle $ABCD$ is the point of intersection of its diagonals.

Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.

$ABCD$ is a cyclic trapezium with $AD\Vert BC$. If $\angle B=70°,$ determine other three angles of the trapezium.

Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).