Section Formula for Internal Division

The line segment joining the points $(3, -1) \mathrm{and} (-6, 5)$ is trisected. The coordinates of the point of trisection are

The coordinates of the mid-point of the line joining the points $\left(x_1, y_1\right)$ and $\left(x_2, y_2\right)$ is

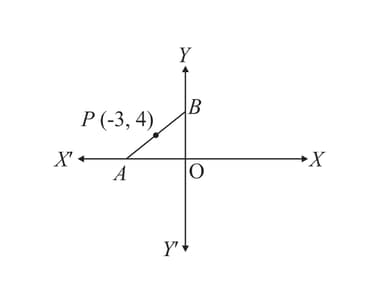
In the figure given below, the line segment $AB$ meets $X-$axis at $A$ and $Y-$axis at $B$. The point $P (-3, 4)$ on $AB$ divides it in the ratio $2 : 3$. Find the coordinates of $A$ and $B$.

If the line joining the points $A( 4,- 5)$ and $B( 4, 5)$ is divided by the point $C$ such that $\frac{AC}{AB}=\frac{3}{5}$, then find the coordinates of $C$.

In what ratio, does the point $(5, 4)$ divide the line segment joining the points $(2, 1)$ and $(7, 6)$?

Find the ratio, in which the line segment joining the points $(- 3, 10)$ and $(6,-8)$ is divided by $(- 1, 6)$.

Find the coordinates of the points of trisection of the line segment joining $(4,-1)$ and $(-2,-3)$.

The line joining points $\mathrm{A}(6, 9)$ and $\mathrm{B}(-6, -9)$ is given. Also, given that two points $\mathrm{P}\left(2, 3\right)$ and $\mathrm{Q}\left(-2, -3\right)$ divide $\overline{\mathrm{AB}}$. What do we call $\mathrm{P}$ and $\mathrm{Q}$ for $\overline{\mathrm{AB}}$? 

Calculate the ratio in which the line joining $\mathrm{A}(5, 6)$ and $\mathrm{B}(-3, 4)$ is divided by $x= 2.$ Also, find the point of intersection.

In what ratio does the point $\mathrm{P}(a, 2)$ divide the line segment joining the points $\mathrm{A}(5,-3)$ and $\mathrm{B}(-9,4)$? Also, find the value of ${}^{\text{'}}\mathrm{a}^{\text{'}}$.

In what ratio does the line $x-y-2=0$ divide the line segment joining the points $(3, -1)$ and $(8, 9) ?$ Also, find co-ordinates of the point of intersection.

The point $\mathrm{P}$ divides the join of $(2,1)$ and $(-3,6)$ in the ratio $2: 3 .$ Does $\mathrm{P}$ lie on the line $x-5y+15=0 ?$

If $\mathrm{P}(9a-2,-b)$ divides the line segment joining the points $\mathrm{A}(3a+1,-3)$ and $\mathrm{B}(8a,5)$ in the ratio $3: 1 ;$ find the values of $\mathrm{a}$ and $\mathrm{b}.$

A line $\mathrm{AB}$ meets the $x$-axis at point $\mathrm{A}$ and $y$-axis at point $\mathrm{B}$. The point $\mathrm{P}(-4,-2)$ divides the line segment $\mathrm{AB}$ internally such that $\mathrm{AP}:\mathrm{PB}=1:2$. Find the co-ordinates of $\mathrm{A}$ and $\mathrm{B}$.

The point, which divides the line segment joining the points $(7,-6)$ and $(3, 4)$ in the ratio $1:2$ internally lies in the

The line $2x+y-4=0$ divides the line segment joining $A(2,-2)$ and $B(3, 7)$ in the ratio

$P$ divides the line segment which joins points $(5, 0)$ and $(0, 4)$ in the ratio of $2: 3$ internally. Co-ordinates of $P$ are :
 

The coordinates of the point $P$ dividing the line segment joining the points $A(1, 3) \text{and} B(4, 6)$ in the ratio $2:1$ are

If the coordinates of the midpoints of the sides $AB, BC$ and $CA$ of a triangle are $(3,4), (1,1)$ and $(2,-3)$respectively, then the vertices $A$ and $B$ of the triangle are

The ratio in which the $\mathrm{x}-$axis divides the line segment joining the points $(6,4)$ and$(1,-7)$ is