Section Formula

If $\mathrm{A}(\frac{m}{3}, 5)$ is the mid-point of the line segment joining the points $\mathrm{Q}(-6, 7)$ and $\mathrm{R}(-2, 3)$, then the value of $m$ is:

 If the point $C\left(-1,2\right)$ divides internally the line segment joining $A\left(2,5\right)$ and $B\left(x,y\right)$ in the ratio $3:4$, find the coordinates of $B$.

Find the ratio in which the segment joining the point $\left(1,-3\right)$ and $\left(4,5\right)$ is divided by $x‐$axis? Also, find the coordinates of this point of the $x‐$axis.

Find the coordinates of a point $A$, where $AB$ is diameter of a circle whose centre is $\left(2,-3\right)$ and $B$ is the point $\left(1,4\right)$. 

$ABC$ is a triangle with vertices $A(1,0), B(5,9)\text{ and }C(9,0)$, Find the coordinates of the midpoints of the three sides of $ABC$.

Find the midpoint of pair of points: $\left(\frac{1}{4},\frac{1}{3}\right)\text{ and }\left(\frac{1}{3},\frac{1}{2}\right)$.

The corners of the Great square of Pegasus are at $(-1,5),(3,2),(-4,1),\text{ and }(0,-2)$.Show that Diagonals bisect each other.

Show that the midpoint of points $U(7,11)\text{ and }V(-2,1)$ lies on the line with equation $y=2x+1$.

Triangle $PQR$ has vertices $P(-2,-3),Q(2,3),\text{ and }R(6,-3)$. $L,M,\text{ and }N$ are the midpoints of $PQ,QR\text{ and }RP$ respectively. Write down the coordinates of $L,M,\text{ and }N$.

Let $A(-1, 5)$ and $B(6, -2)$ be two given points. Find the coordinates of the point $P$ such that $AP=\frac{3}{7}AB$ and $P$ lies on $AB$.

Find the coordinates of the point which divides the line joining $(1 ,-2)$ and $(4, 7)$ internally in the ratio $1:2$

Find the coordinates of the point which divides the line segment joining the points $(6,3)$ and $(-4,5)$ in the ratio $3:2$ internally.

$P \text{and} Q$ are such two points on the line segment obtained by joining the points $A\left(-2, 5\right) \text{and} B\left(3, 1\right)$ that $AP=PQ=QB$. Then find the coordinates of the midpoint of $PQ$. 

If the points $P\left(a, 1\right), Q\left(1, b\right), R\left(-2, 11\right)$ are collinear and $Q$ be the midpoint of $\overline{PR}$, then find the value of $a \text{and} b$.

The straight line $4x+3y-k=0$ intersects the $x-$axis and $y-$axis at $A \text{and} B$, respectively. Find the coordinates of the point at which the straight line $\overline{AB}$ is divided internally into the ratio $2:1$. 

The coordinates of the midpoint of the line segment obtained by joining the points $\left(l, m\right)$ and $\left(l+m, l-m\right)$ are _____.

Find the coordinates of the points of trisection of the line segment joining the points $A(-5,6)$ and $B(4,-3)$.

The coordinates of the point which is equidistant from the three vertices of the $∆AOB$ as shown in the figure are

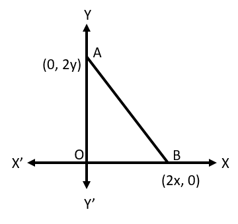
A line intersects the $y$-axis and$x$-axis at the points $P$ and $Q$, respectively. If $(2, -5)$ is the mid-point of $PQ$, then the coordinates $P$ and $Q$ are respectively

The line $2x+y-4=0$ divides the line segment joining $A\left(2, -2\right)$ and $\left(3, 7\right)$ in the ratio