Embibe Experts Solutions for Chapter: Linear Programming, Exercise 1: Exercise 1

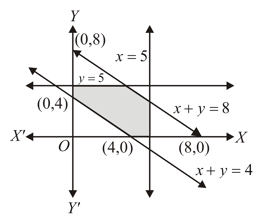
Linear inequalities for which the shaded region of the given figure is the solution set, are

There is a factory located at each of the two places $P$ and $Q$. From these locations, a certain commodity is delivered to each of the three depots situated at $A,B$ and $C$. The weekly requirements of the depots are respectively, $5, 5$ and $4$ units commodity, while the production capacity of the factories at $P$ and $Q$ are $8$ and $6$ units, respectively. The cost of transportation per unit is given below:

Formulate the $\mathrm{L}.\mathrm{P}.\mathrm{P}.$, so that the units transported from each factory to each depot in such an order that the transportation cost is minimum.

A farmer mixes two brands $P$ and $Q$ of cattle feed. Brand $P$, costing $₹ 250$ per bag, contains $3$ units of nutritional element $A, 2.5$ units of element $B$ and $2$ units of element $C$ Brand $Q$ costing $₹200$ per bag contains $1.5$ units of nutritional element $A, 11.25$  units of elements $B$ and $3$ units of element $C$. The minimum requirements of nutrients $A,B$ and $C$ are $18$ units, $45$ units and $24$ units, respectively. Then, the minimum cost is

A firm has to transport $1200$ packages using large vans which can carry $200$ packages each and small vans which can take $80$ packages each. The cost for engaging each large van is $₹400$ and each small van is $₹200$. Not more than $₹3000$ is to be spent on the job and the number of large vans cannot exceed the number of small vans. Then, the minimum cost for the firm is

A manufacturer has three machines $\mathrm{I}, \mathrm{II}$ and $\mathrm{III}$ installed in his factory. Machines $\mathrm{I}$ and $\mathrm{II}$ are capable of being operated for utmost $12$ hours  whereas, machine $\mathrm{III}$ must be operated for at least $5$ hours a day. She produces only two items $M$ and $N$ each requiring the use of all the three machines.

The number of hours required for producing $\mathrm{I}$ unit of each of $M$ and $N$ on the three machines are given in the following table:

She makes a profit of $₹600$ and $₹400$ on items $M$ and $N$, respectively,

Then, to maximise the profit, number of units of item $M$, the manufacturer has to produce, is

Anil wants to invest utmost $₹12000$ is bonds $A$ and $B$. According to the rules, he has to invest at least $₹2000$ in bond $A$ and at least $₹4000$ in bond $B$. If the rate of interest in bond $A$ is $8\%$ per annum and in bond $B$ is $10\%$ per annum, then to maximise the interest, the investment in bond $A$ and $B$ are respectively

Reshma wishes to mix two types of food $P$ and $Q$ in such a way that the vitamin contents of the mixture contain at least $8 \mathrm{units}$ of vitamin $A$ and $11 \mathrm{units}$  of vitamin $B$. Food $P$ costs $₹60/\mathrm{kg}$ and food $Q$  costs $₹80/\mathrm{kg}$. Food $P$ contains $3 \mathrm{units}/\mathrm{kg}$  of vitamin $A$ and $5 \mathrm{units}/\mathrm{kg}$ of vitamin $B$, while food $Q$ contains $4 \mathrm{units}/\mathrm{kg}$ of vitamin $A$ and $2 \mathrm{units}/\mathrm{kg}$ of vitamin $B$. Then, the minimum cost of the mixture is

The linear programming problem Maximise $Z=x_1+x_2$ subject to constraints are $x_1+2x_2\le 2000, x_1+x_2\le 1500, x_2\le 600$,

$x_1\ge 0$ and $x_2\ge 0$ has