Area of Sectors and Segments of a Circle

Two concentric circles have radii $6 \mathrm{cm}$ and $4 \mathrm{cm}$. A sector of $60°$ is drawn in each circle. Find the difference between the areas of the two sectors. Write the answer in ${\mathrm{cm}}^2$ (round off to two decimal places). (use $\mathrm{\pi }=3.14$)

Find the area of a sector of a circle of radius $14 \mathrm{cm}$ when the sectorial angle is $120°$. Write the answer in ${\mathrm{cm}}^2$ (round off to two decimal places).(use $\mathrm{\pi }=\frac{22}{7}$)

Find the area of a sector of a circle of radius $14 \mathrm{cm}$ when the sectorial angle is $90°$. Write the answer in ${\mathrm{cm}}^2$.(use $\mathrm{\pi }=\frac{22}{7}$)

Find the area of a sector of a circle of radius $14 \mathrm{cm}$ when the sectorial angle is $60°$. Write the answer in ${\mathrm{cm}}^2$ (round off to two decimal places).(use $\mathrm{\pi }=\frac{22}{7}$)

Find the area of a sector of a circle of radius $14 \mathrm{cm}$ when the sectorial angle is $45°$. Write the answer in ${\mathrm{cm}}^2$.(use $\mathrm{\pi }=\frac{22}{7}$)

Find the area of a sector of a circle of radius $14 \mathrm{cm}$ when the sectorial angle is $30°$. Write the answer in ${\mathrm{cm}}^2$ (round off to two decimal places). (use $\mathrm{\pi }=\frac{22}{7}$)

The minute hand of a clock is $4.2 \mathrm{cm}$ long. Find the area swept by it in $20$ minutes. Write the answer in ${\mathrm{cm}}^2$ (round off to two decimal places).(use $\mathrm{\pi }=\frac{22}{7}$)

Find the sectorial angle and area of the sector of a circle if the arc length of the corresponding sector is $8.8 \mathrm{cm}$ and the radius of the circle is $5.6 \mathrm{cm}$.(use $\mathrm{\pi }=\frac{22}{7}$)

The area of a sector of a circle of radius $21 \mathrm{cm}$ is $462 {\mathrm{cm}}^2$. Find the length of the arc of the sector. Write the answer in ${\mathrm{cm}}^2$.(use $\mathrm{\pi }=\frac{22}{7}$)

The circumference of a circle is $176 \mathrm{cm}$. Find the area of a sector whose sectorial angle is $45°$. Write the answer in ${\mathrm{cm}}^2$.(use $\mathrm{\pi }=\frac{22}{7}$)

The radius of a circle is $6 \mathrm{cm}$ and the area of a sector of this circle is $18\frac{6}{7} {\mathrm{cm}}^2$. If the angle of the sector is $k°$, then find the value of $k$.(use $\mathrm{\pi }=\frac{22}{7}$)

The perimeter of a certain sector of a circle of radius $6.5 \mathrm{cm}$ is $21 \mathrm{cm}$. Find the area of the sector. Write the answer in ${\mathrm{cm}}^2$ (round off to two decimal places).(use $\mathrm{\pi }=\frac{22}{7}$)

Semi-circles are described on the sides $AB \text{and} CD$ of a rectangle $ABCD$ as diameters, both inside the rectangle. If $AB=14 \mathrm{cm}$ and $BC=7 \mathrm{cm}$, find the area of the portion of the rectangle lying outside the semi-circles. 

Semi-circles are described on the sides $AB \text{and} CD$ of a rectangle $ABCD$ as diameters, both inside the rectangle. If $AB=14 \mathrm{cm}$ and $BC=7 \mathrm{cm}$, find the area enclosed by the-semi circles.

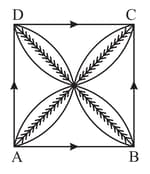
$ABCD$ is a square of side $7 \mathrm{cm}$ and semi-circles are drawn with each side of the square as diameter, thereby forming four similar petals as shown in the adjoining figure. Find the cost of making design on the petals at the rate of $₹12$ per square centimetre. 

A grass field is in the form of an equilateral triangle of sides $48 \mathrm{m}$. A cow can tether at a vertex of the field. If the cow can reach up to $21 \mathrm{m}$ from the vertex, find the increase in grazing area if the length of the rope be increased to $35 \mathrm{m}$. (use $\mathrm{\pi }=3.14$)

A grass field is in the form of an equilateral triangle of sides $48 \mathrm{m}$. A cow can tether at a vertex of the field. If the cow can reach up to $21 \mathrm{m}$ from the vertex, find how much area remains ungrazed. (Correct upto two decimal places)

A grass field is in the form of an equilateral triangle of sides $48 \mathrm{m}$. A cow can tethered at a vertex of the field. If the cow can reach upto $21 \mathrm{m}$ from the vertex, find the area of the part of the field in which the cow can graze.

A chord of a circle subtends an angle of $60°$ at the centre. If the length of the chord is $12 \mathrm{cm}$, find the area of the two segments into which the chord divides the circle (take $\mathrm{\pi }=3.14$ and $\sqrt{3}=1.73$)

The chord of a circle of diameter $12 \mathrm{cm}$ makes an angle of $30°$ at the centre. Find the area of the minor segment of the circle. (Correct upto two decimal places)