Mid-Point and Intercept Theorems
Important Questions on Mid-Point and Intercept Theorems
In and are the midpoint of and respectively. If , and , find the value of .
In and are the midpoint of and respectively. If , and , if the value of then find .
In and are the midpoint of and respectively. If , and , find the value of .
In and are the midpoint of and respectively. If , , and , then find the value of .
In a , the medians and are produced to points and , respectively such that and . Prove that and are collinear.
is a trapezium with and is midpoint of . If meets . Prove that is the midpoint of .
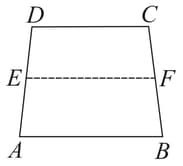
On , is obtuse. are the midpoints of respectively and is a point on such that . Prove that is a parallelogram.
In a , the medians and are produced to points and , respectively such that and . Prove that is the midpoint of .
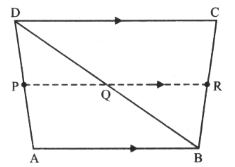
is a parallelogram and are the midpoint of and , respectively, is any line that intersects , and at , and respectively. Prove that .
The diagonals of a quadrilateral intersect at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.
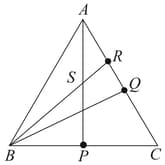
In parallelogram , is the mid point of side and is drawn parallel to , which meets produced at and cuts side at . Prove that .
In parallelogram , is the mid point of side and is drawn parallel to , which meets produced at and cuts side at . Prove that .
In , is the mid point of . Prove that .
In the given figure is a trapezium in which . is the mid point of and . Prove that: .
is a median of , is the mid-point of . produced meet at . . Prove that .
Prove that the four triangles formed by joining the mid-point of the sides are congruent to each other.
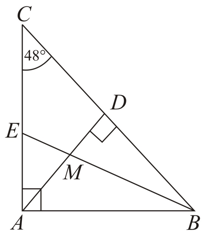
In the adjoining figure, , bisector of . and intersect at . Calculate .
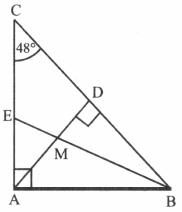
In the adjoining figure, , . bisector of , and intersect at . Calculate .