The Mid-point Theorem

$\mathrm{A}\mathrm{B}\mathrm{C}$ is a triangle right-angled at $\mathrm{C}.$ A line through the midpoint $\mathrm{M}$ of hypotenuse $\mathrm{A}\mathrm{B}$ and parallel to $\mathrm{B}\mathrm{C}$ intersects $\mathrm{A}\mathrm{C}$ at $\mathrm{D}.$ Show that $\mathrm{D}$ is the midpoint of $\mathrm{A}\mathrm{C}$.
 

$\mathrm{A}\mathrm{B}\mathrm{C}$ is a triangle right-angled at $\mathrm{C}.$ A line through the midpoint $\mathrm{M}$ of hypotenuse $\mathrm{A}\mathrm{B}$ and parallel to $\mathrm{B}\mathrm{C}$ intersects $\mathrm{A}\mathrm{C}$ at $\mathrm{D}.$ Show that $\mathrm{C}\mathrm{M}=\mathrm{M}\mathrm{A}=\frac{1}{2}\mathrm{A}\mathrm{B}$

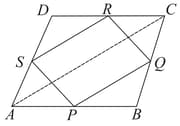
$\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ is a quadrilateral in which $\mathrm{P}, \mathrm{Q}, \mathrm{R}$ and $\mathrm{S}$  are mid-points of the sides $\mathrm{A}\mathrm{B}, \mathrm{B}\mathrm{C}, \mathrm{C}\mathrm{D}$ and $\mathrm{D}\mathrm{A}$. $\mathrm{A}\mathrm{C}$ is a diagonal. Show that: $\mathrm{P}\mathrm{Q}\mathrm{R}\mathrm{S}$ is a parallelogram.

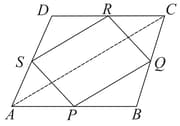
$\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ is a quadrilateral in which $\mathrm{P}, \mathrm{Q}, \mathrm{R}$ and $\mathrm{S}$ are mid-points of the sides $\mathrm{A}\mathrm{B}, \mathrm{B}\mathrm{C}, \mathrm{C}\mathrm{D}$ and $\mathrm{D}\mathrm{A}$. $\mathrm{A}\mathrm{C}$ is a diagonal. Show that: $\mathrm{P}\mathrm{Q}=\mathrm{S}\mathrm{R}$
 

$\mathrm{A}\mathrm{B}\mathrm{C}$ is a triangle right-angled at $\mathrm{C}.$ A line through the midpoint $\mathrm{M}$ of hypotenuse $\mathrm{A}\mathrm{B}$ and parallel to $\mathrm{B}\mathrm{C}$ intersect $\mathrm{A}\mathrm{C}$ at $\mathrm{D}.$ Show that $\mathrm{M}\mathrm{D}\perp \mathrm{A}\mathrm{C}$
 

Show that the line segments joining the midpoints of the opposite sides of a quadrilateral bisect each other.

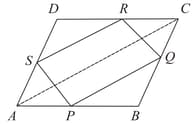
In a parallelogram $\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}, \mathrm{E}$ and $\mathrm{F}$ are the mid-points of sides $\mathrm{A}\mathrm{B}$ and $\mathrm{C}\mathrm{D}$ respectively. Show that the line segments $\mathrm{A}\mathrm{F}$ and $\mathrm{E}\mathrm{C}$ trisect the diagonal $\mathrm{B}\mathrm{D}$
​​​​​​​

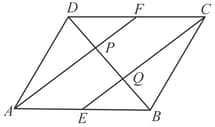
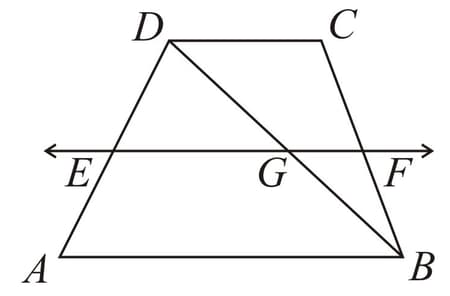
$\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ is a trapezium in which $\mathrm{A}\mathrm{B}\parallel \mathrm{D}\mathrm{C}, \mathrm{B}\mathrm{D}$ is a diagonal and $\mathrm{E}$ is the midpoint of $\mathrm{A}\mathrm{D}.$ A line is drawn through $\mathrm{E}$ parallel to $\mathrm{A}\mathrm{B}$ intersecting $\mathrm{B}\mathrm{C}$ at $\mathrm{F}$. Show that $\mathrm{F}$ is the midpoint of $\mathrm{B}\mathrm{C}.$

$\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ is a rectangle and $\mathrm{P}, \mathrm{Q}, \mathrm{R}$ and $\mathrm{S}$ are mid-points of the sides $\mathrm{A}\mathrm{B}, \mathrm{B}\mathrm{C}, \mathrm{C}\mathrm{D}$ and $\mathrm{D}\mathrm{A}$ respectively. Show that the quadrilateral $\mathrm{P}\mathrm{Q}\mathrm{R}\mathrm{S}$ is a rhombus.

$\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ is a rhombus and $\mathrm{P}, \mathrm{Q}, \mathrm{R}$, $\mathrm{S}$ are the midpoints of the sides $\mathrm{A}\mathrm{B}, \mathrm{B}\mathrm{C}, \mathrm{C}\mathrm{D}$ and $\mathrm{D}\mathrm{A}$ respectively. Show that the quadrilateral $\mathrm{P}\mathrm{Q}\mathrm{R}\mathrm{S}$ is a rectangle.

$\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$ is a quadrilateral in which $\mathrm{P}, \mathrm{Q}, \mathrm{R}$ and $\mathrm{S}$ are mid-points of the sides $\mathrm{A}\mathrm{B}, \mathrm{B}\mathrm{C}, \mathrm{C}\mathrm{D}$ and $\mathrm{D}\mathrm{A}$. $\mathrm{A}\mathrm{C}$ is a diagonal. Show that: $\mathrm{S}\mathrm{R}\parallel \mathrm{A}\mathrm{C}$ and $\mathrm{S}\mathrm{R}=\frac{1}{2}\mathrm{A}\mathrm{C}$