Michele Conway, Belle Cottingham, Alastair Duncombe and, Amanda George Solutions for Exercise 7: Exercise 3
Michele Conway Mathematics Solutions for Exercise - Michele Conway, Belle Cottingham, Alastair Duncombe and, Amanda George Solutions for Exercise 7: Exercise 3
Attempt the free practice questions from Exercise 7: Exercise 3 with hints and solutions to strengthen your understanding. Cambridge Lower Secondary Maths Stage 9: Student's Book solutions are prepared by Experienced Embibe Experts.
Questions from Michele Conway, Belle Cottingham, Alastair Duncombe and, Amanda George Solutions for Exercise 7: Exercise 3 with Hints & Solutions
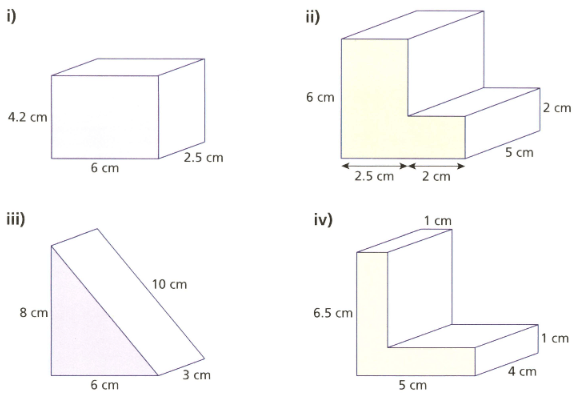
Calculate the surface area (in ) of the following prisms. And, complete the Venn diagram below.
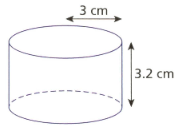
Calculate the surface area (in ) of the following cylinder. (Use, )
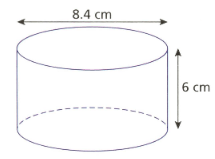
Calculate the surface area (in ) of the following cylinder. Write the answer to the nearest whole number (Use, )
Calculate the surface area (in ) of the following cylinder. (Use, )
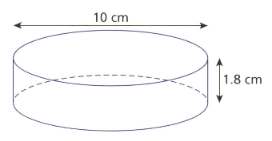
Mr wilson's pencil pot is in the shape of a cylinder. He decorates the surface area of the pot including the base. What is the pot's total (outside) surface area (in )? (Use, )
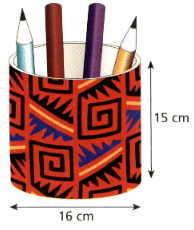
Ben thinks that the surface area of this prism equals the sum of the surface areas the two cuboids. Is he correct? Show your workings clearly.
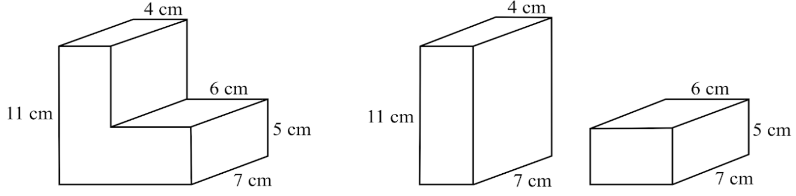
These shapes have an equal surface area. Calculate the missing length (in ).
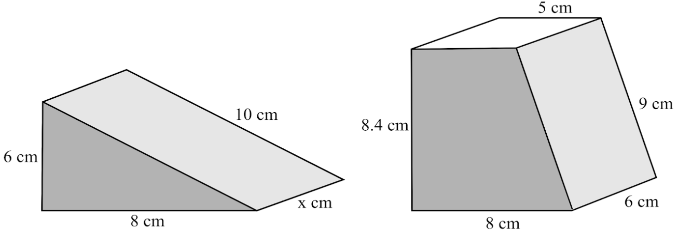
Is it true, sometimes or never true?
If two cylinders have equal volumes, their surface areas are equal too. Justify your answer.
