J P Mohindru and Bharat Mohindru Solutions for Chapter: Areas Related to Circles, Exercise 2: EXERCISE

An arc of length $20\mathrm{\pi } \mathrm{cm}$ subtends an angle of $144°$ at the centre of circle. Find the radius of the circle.

What is the perimeter of a sector of angle $45°$ of a circle with radius $7 \mathrm{cm}$? (Use $\pi =\frac{22}{7}$)

A chord $AB$ of a circle, of radius $14 \mathrm{cm}$ makes an angle of $60°$ at the centre of the circle. The area of the minor segment of the circle is $\mathrm{k} {\mathrm{cm}}^2$. Find the value of $\mathrm{k}$.

(Use $\mathrm{\pi }=\frac{22}{7}$)

The minute hand of a clock is $7 \mathrm{cm}$ long. The area of the face of the clock by the minute hand between $9 \mathrm{A}.\mathrm{M}.$ and $9.35 \mathrm{A}.\mathrm{M}.$ is $\mathrm{k} {\mathrm{cm}}^2$. Find the value of $\mathrm{k}$.

The short and long hands of a clock are$4 \mathrm{cm}$ and $6 \mathrm{cm}$ long respectively. If the sum of distances travelled by their tips in$2$ days is $k \mathrm{cm}$, then find the value of $k$. (Take $\mathrm{\pi }=\frac{22}{7}$)

The diagram shows a sector of a circle of radius $r$ making an angle $\theta °$. The area of the sector is $A {\mathrm{cm}}^2$ and perimeter of the sector is $50 \mathrm{cm}$.

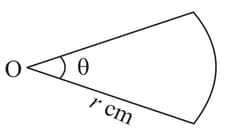
Prove that: $A=25r-r^2$
                                  

The area of the segment $AYB$ (shown in figure), if the radius of the circle is $21 \mathrm{cm}$ and $\angle AOB=120°$, is $\mathrm{k} {\mathrm{cm}}^2$. Find the value of $\mathrm{k}$. (Use $\pi =\frac{22}{7}$)

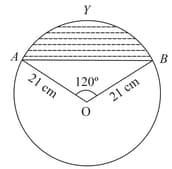
A chord of a circle is of radius $12 \mathrm{cm}$ subtends an angle of $120°$ at the centre. Find the area of the corresponding segment of the circle (in ${\mathrm{cm}}^2$).
(Use $\mathrm{\pi }=3.14$ and $\sqrt{3}=1.73$)