J P Mohindru and Bharat Mohindru Solutions for Chapter: Areas Related to Circles, Exercise 3: EXERCISE

In adjoining figure, a letter block of letter $\text{'}P\text{'}$ is shown which is uniformly broad throughout. The column is rectangular and curved portion is semicircular. The area of shaded portion is $k {\mathrm{cm}}^2$. Find the value of $k$.

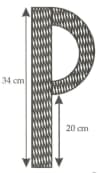
*Note: The given question in the textbook is incomplete, the correct complete question is written below*

In adjoining figure, a letter block of letter $\text{'}P\text{'}$ is shown which is uniformly broad throughout. The column is rectangular and curved portion is semicircular and the width of strip is $3 \mathrm{cm}$.The area of shaded portion is $k {\mathrm{cm}}^2$. Find the value of $k$.(Correct answer up to two decimal places).

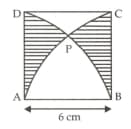
In the fig., $ABCD$ is a square of side $6 \mathrm{cm}$. The area of the shaded region is $k {\mathrm{cm}}^2$. Use, $\mathrm{\pi }=\frac{22}{7}, \sqrt{3}=1.732$ (Correct answer up to two decimal places).Find the value of $k$.

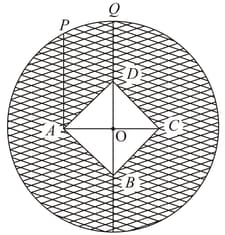
In the figure, $ABCD$ is a square inside a circle $O$. The centre of the square coincide with $O$ and the diagonal $AC$ is horizontal of $AP, ODQ$ is vertical and $AP=45 \mathrm{cm} , DQ=25 \mathrm{cm}$. Find side of square. (Use $\pi =3.14, \sqrt{2}=1.41$)

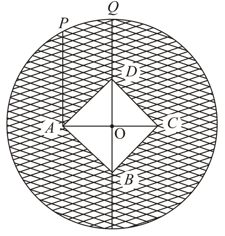
In the figure, $ABCD$ is a square inside a circle $O$. The centre of the square coincide with $O$ and the diagonal $AC$ is horizontal of $AP, ODQ$ is vertical and $AP=45 \mathrm{cm} , DQ=25 \mathrm{cm}$. The area of shaded region is $k c{m}^2$. (Use $\pi =3.14, \sqrt{2}=1.41$). Find the value of $k$.

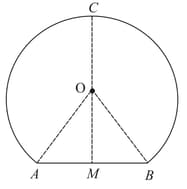
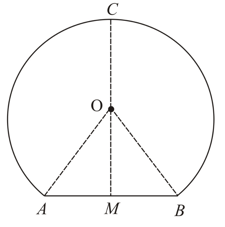
The figure shows the cross-section of a railway tunnel. The radius of the tunnel is $3.5 \mathrm{m}$ (i.e, $OA=3.5 \mathrm{m}$) and ­$AOB=90°$. Calculate the height of the tunnel.

The figure shows the cross-section of a railway tunnel. The radius of the tunnel is $3.5 \mathrm{m}$ (i.e, $OA=3.5 \mathrm{m}$) and ­$AOB=90°$. Calculate the perimeter of its cross-section, including base.

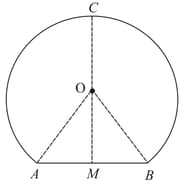
The figure shows the cross-section of a railway tunnel. The radius of the tunnel is $3.5 \mathrm{m}$ (i.e, $OA=3.5 \mathrm{m}$) and ­$AOB=90°$. If the area of the cross-section is $k {\mathrm{m}}^2$ then find $k$.

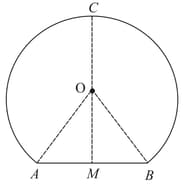
The figure shows the cross-section of a railway tunnel. The radius of the tunnel is $3.5 \mathrm{m}$ (i.e, $OA=3.5 \mathrm{m}$) and ­$AOB=90°$. The internal surface area of the tunnel, excluding base, if its length is $50 \mathrm{m}$ is $k {\mathrm{m}}^2$. Find the value of $k$.