Cyclic Quadrilaterals

A quadrilateral $ABCD$is inscribed in a circle such that$AB$ is diameter and $\angle ADC={130}^{°}.$ If $\angle BAC=k°$, then write the value of $k$.

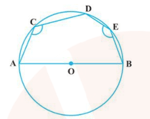
In Figure, $\angle ADC=130°$ and chord $BC=$chord $BE$. If $\angle CBE=k°$. Then find the value of k.

In Figure, $AOB$ is a diameter of the circle and $C,D, E$ are any three points on the semi-circle. If the value of $\angle ACD+\angle BED=k°$. Then find the value of $k$.

If bisectors of opposite angles of a cyclic quadrilateral $ABCD$ intersect the circle, circumscribing it at the points $P$ and $Q$, prove that $PQ$ is a diameter of the circle.

$ABCD$ is a parallelogram. A circle through $A, B$ is so drawn that it intersects $AD$ at $P$ and$BC$ at $Q$. Prove that $P, Q, C$and$D$ are concyclic.

If non-parallel sides of a trapezium are equal, prove that it is cyclic.

If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral so formed is cyclic.

On a common hypotenuse $AB$, two right triangles $ACB$ and $ADB$ are situated on opposite sides, Prove that $\angle \mathrm{BAC}=\angle \mathrm{BDC}$.

In the given figure, if $AOB$ is a diameter and $\angle ADC=120°,$ then $\angle CAB=30°.$

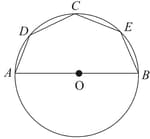
$ABCD$ is a cyclic quadrilateral such that $\angle A=90°,\angle B=70°,\angle C=95°$ and $\angle D=105°$.

$\mathrm{ABCD}$ is a cyclic quadrilateral such that $\mathrm{AB}$ is a diameter of the circle circumscribing it and $\angle \mathrm{ADC}=140°$, then $\angle \mathrm{BAC}$ is equal to