Properties of a Parallelogram
Properties of a Parallelogram: Overview
In this topic, we will study the properties of a parallelogram with the help of examples and exercises. We will also learn about the execution of these properties in solving the problems which will help to enhance our skills.
Important Questions on Properties of a Parallelogram
is a rhombus in which altitude from to side bisects . Find the angles of the rhombus.
The angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is . Find the angles of the
parallelogram.
Diagonals and of a parallelogram intersect each other at . If and determine the lengths of and .
In the given figure, and are two parallelograms.
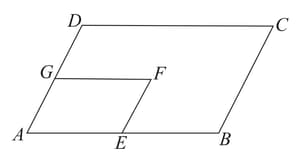
If and , then find the value of .
Opposite angles of a quadrilateral are equal. If and , then find the value of .
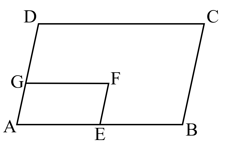
Diagonals of a quadrilateral bisect each other. If and , then find the value of .
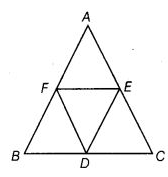
and are respectively the mid-points of the sides and of a triangle . Prove that by joining these mid-points and , the triangle is divided into four congruent triangles.
and are points on opposite sides and of a parallelogram such that passes through the point of intersection of its diagonals and . Show that is bisected at .
In the given figure, and . Prove that and .
and are the midpoints of the opposite sides and of a parallelogram . intersects at and intersects at . Show that is a parallelogram.
A diagonal of a parallelogram bisects one of its angles. Show that it is a rhombus.
In the given figure, is the midpoint of side of a parallelogram such that . Prove that .
Through and lines and have been drawn, respectively parallel to sides and of a as shown in the given figure. Show that .
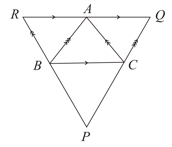
and are points on diagonal of a parallelogram such that . Show that is a parallelogram.
In the given figure, it is given that and are parallelograms. Can you say that ? Why or why not?
Diagonals of a rectangle are equal and perpendicular. Is this statement true? Give reason for your answer.
All the angles of a quadrilateral are equal. What special name is given to this quadrilateral?
Diagonals of a parallelogram are perpendicular to each other. Is this statement true? Give reason for your answer.
Which of the following is not true for a parallelogram?
The figure formed by joining the mid-points of the sides of a quadrilateral , taken in order, is a square only, if
