Motional Electromotive Force

A long solenoid '$\mathrm{S}$’ has '$n$’ turns per meter, with diameter '$a$'. At the centre of this coll we place a smaller coil of ‘$N$' turns and diameter ‘$b$’ (where $b<a$). If the current In the solenoid increases linearly, with time, what is the Induced emf appearing In the smaller coil. Plot graph showing nature of variation in emf. If current varies as a function of $m{t}^2+C$.

A metallic ring of mass $m$ and radius $l$ (ring being horizontal) Is falling under gravity In a region having a magnetic Held. If $z$ Is the vertical direction, the $z$-component of magnetic field is $B_x=B_0(1+\lambda z)$. If $R$ Is the resistance of the ring and If the ring falls with a velocity $v$, find the energy lost In the resistance. If the ring has reached a constant velocity, use the conservation of energy to determine uln terms of $m, B, \lambda$ and acceleration due to gravity $g$.

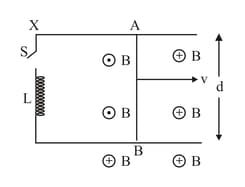
Find the current in the sliding rod $\mathrm{AB}$ (resistance$=\mathrm{R}$) for the arrangement shown in Figure. $\mathrm{B}$ is constant and is out of the paper. Parallel wires have no resistance, $v$ is constant. Switch $\mathrm{S}$ is closed at time $t=0$.

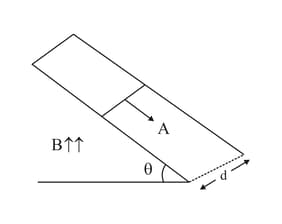
A rod of mass $m$ and resistance $R$ slides smoothly over two parallel perfectly conducting wires kept sloping at an angle $\theta$ with respect to the horizontal (Figure). The circuit is closed through a perfect conductor at the top. There is a constant magnetic field $\mathrm{B}$ along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.

A magnetic field $\mathrm{B}$ is confined to a region $r\le a$ and points out of the paper (the $z$-axis). $r=0$ being the centre of the circular region. A charged ring (charge $=Q$) of radius $b, b>a$ and mass $m$ lies in the $x$-$y$ plane with its centre at the origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time $∆t$. Find the angular velocity $\omega$ of the ring after the field vanishes.

A rectangular loop of wire $\mathrm{ABCD}$ is kept close to an infinitely long wire carrying a current $I\left(t\right)=I_0(1-t/T)$ for $0\le t\le T$ and $I\left(0\right)=0$ for $t>T$ (Figure). Find the total charge passing through a given point in the loop, in time $T$. The resistance of the loop is $R$.

Consider an infinitely long wire carrying a current $I\left(t\right)$. with $\frac{dI}{dt}=\lambda =$constant.

Find the current produced in the rectangular loop of wire $\mathrm{ABCD}$ if its resistance is $R$ (figure).

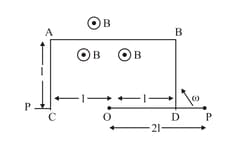
$\mathrm{ODBAC}$ is a fixed rectangular conductor of negligible resistance ($\mathrm{CO}$ is not connected) and $\mathrm{OP}$ is a conductor which rotates clockwise with an angular velocity to (Figure). The entire system is in a uniform magnetic field $\mathrm{B}$ whose direction is along the normal to the surface of the rectangular conductor $\mathrm{ABDC}$. The conductor $\mathrm{OP}$ is in electric contact with $\mathrm{ABDC}$. The rotating conductor has a resistance of $\mathrm{\lambda }$ per unit length. Find the current in the rotating conductor, as it rotates by $180°$.

A magnetic field $\mathrm{B}=B_0\sin \left(\omega t\right)\hat{\mathrm{k}}$ covers a large region where a wire $\mathrm{AB}$ slides smoothly over two parallel conductors separated by a distance $d$ (Figure). The wires are in the $x-y$ plane. The wire $\mathrm{AB}$(of length $d$) has resistance $R$ and the parallel wires have negligible resistance. If $\mathrm{AB}$ is moving with velocity $v$, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity?

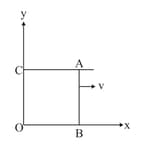
A (current vs time) graph of the current passing through a solenoid is shown in Figure. For which time is the back electromotive force $\left(u\right)$ a maximum. If the back e.m.f. at $t=3\mathrm{s}$ is $e$. find the back e.m.f. at $t=7\mathrm{s}, 15\mathrm{s}$ and $40\mathrm{s}$. $\mathrm{OA}, \mathrm{AB}$ and $\mathrm{BC}$ are straight line segments.

A circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because

Same as problem $4$ except the coil $\mathrm{A}$ is made to rotate about a vertical axis (figure). No current flows in $\mathrm{B}$ if $\mathrm{A}$ is at rest. The current in coil $\mathrm{A}$, when the current in $\mathrm{B}$ (at $t=0$) is counterclockwise and the coil $\mathrm{A}$ is as shown at this instant, $t=0$, is

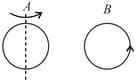
There are two coils $\mathrm{A}$ and $\mathrm{B}$ as shown in Figure. A current starts flowing in $\mathrm{B}$ as shown, when $\mathrm{A}$ stops moving. The current in $\mathrm{A}$ is counterclockwise. $\mathrm{B}$ is kept stationary when $\mathrm{A}$ moves. We can infer that