NCERT Solutions for Chapter: Areas of Parallelograms and Triangles, Exercise 4: Exercise
NCERT Mathematics Solutions for Exercise - NCERT Solutions for Chapter: Areas of Parallelograms and Triangles, Exercise 4: Exercise
Attempt the free practice questions on Chapter 9: Areas of Parallelograms and Triangles, Exercise 4: Exercise with hints and solutions to strengthen your understanding. NCERT Exemplar Mathematics - Class 9 solutions are prepared by Experienced Embibe Experts.
Questions from NCERT Solutions for Chapter: Areas of Parallelograms and Triangles, Exercise 4: Exercise with Hints & Solutions
The medians and of a triangle intersect at . Prove that the area of area of the quadrilateral .
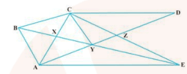
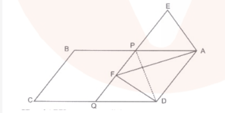
In given figure, and . Prove that
is a trapezium in which and . If and are respectively the mid-points of and , prove that: .
In , if and are the points on and , respectively such that Prove that .
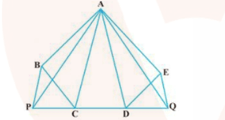
In the given figure, is any pentagon. drawn parallel to meets produced at and drawn parallel to meets produced at Prove that
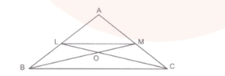
If the medians of a intersect at show that
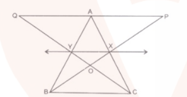
In given figure, and are the midpoints of and respectively, and and are straight lines. Prove that .
In the given figure, and are two parallelograms. Prove that . [ Hint: join ]