Relation between Electric Current and Drift Velocity: Derivation of Ohm's Law

The diagram below shows a potentiometer set up. On touching the jockey near to the end $X$ of the potentiometer wire, the galvanometer pointer.

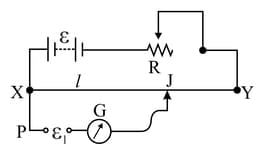
deflects to left. On touching the jockey near to end $Y$ of the potentiometer, the galvanometer pointer again deflects to left but now by a larger amount. Identify the fault in the circuit and explain, using appropriate equations or otherwise, how it leads to such a one-sided deflection.

Two material bars $A$ and $B$ of equal area of cross-section, are connected in series to a $DC$ supply. A is made of usual resistance wire and $B$ of an $n$-type semiconductor.

If the same constant current continues to flow for a long time, how will the voltage drop across $A$ and $B$ be affected ?
Justify each answer.

Two material bars $A$ and $B$ of equal area of cross-section, are connected in series to a $DC$ supply. A is made of usual resistance wire and $B$ of an $n$-type semiconductor.
In which bar is drift speed of free electrons greater ?

Derive an expression for drift velocity of free electrons.

State the two Kirchhoff's rules used in electric networks. How are these rules justified?

What is a safety fuse? Explain its function.

Give four reasons why nichrome element is commonly used in household heating appliances.

Two heating elements of resistances $R_1$ and $R_2$ when operated at a constant supply of voltage, $V,$ consume powers $P_1$ and $P_2$ respectively. Deduce the expressions for the power of their combination when they are, in turn, connected in parallel across the same voltage supply.

Two heating elements of resistances $R_1$ and $R_2$ when operated at a constant supply of voltage, $V,$ consume powers $P_1$ and $P_2$ respectively. Deduce the expressions for the power of their combination when they are, in turn, connected in series.

Obtain the formula for the 'power loss' in a conductor of resistance $R,$ carrying a current $I.$

Clarify your elementary notions about current in a metallic conductor by answering the following queries:

If the electron drift speed is so small, and the electron's charge is small, how can we still obtain large amounts of current in a conductor?

Mobilities of electrons and holes in a sample of intrinsic germanium at room temperature are $0.54 {\mathrm{m}}^2{\mathrm{V}}^{-1}{\mathrm{s}}^{-1}$ and $0.18 {\mathrm{m}}^{-1}{\mathrm{V}}^{-1}{\mathrm{s}}^{-1}$ respectively. If the electron and hole densities are equal to $3.6\times {10}^{19}{\mathrm{m}}^{-3}$ calculate the germanium conductivity.

The number density of electrons in copper is $8.5\times {10}^{28}{\mathrm{m}}^{-3}$ A current of $1 \mathrm{A}$ flows through a copper wire of length $0.24 \mathrm{m}$ and area of cross-section $1.2 {\mathrm{mm}}^2$, when connected to a battery of $3 \mathrm{V}$. Find the electron mobility.

A potential difference of $4.5 \mathrm{V}$ is applied across a conductor of length $0.1 \mathrm{m}$. If the drift velocity of electrons is $1.5\times {10}^{-4}{\mathrm{m} \mathrm{s}}^{-1}$, find the electron mobility.

When a potential difference of $1.5 \mathrm{V}$ is applied across a wire of length $0.2 \mathrm{m}$ and area of cross-section $0.3 {\mathrm{mm}}^2$, a current of $2.4 \mathrm{A}$ flows through the wire. If the number density of free electrons in the wire is $8.4\times {10}^{28}{\mathrm{m}}^{-3}$, calculate the average relaxation time. Given that mass of electron $=9.1\times {10}^{-31}\mathrm{kg}$ and charge on electron $=1.6\times {10}^{-19}\mathrm{C}$.

What is the drift velocity of electrons in the silver wire of length $1 \mathrm{m}$, having cross-sectional area $3.14\times {10}^{-6}{\mathrm{m}}^2$ and carrying a current of $10 \mathrm{A}$? Given atomic mass $=108$, density of silver $10.5\times {10}^3\mathrm{kg} {\mathrm{m}}^{-3}$, charge on electron $=1.6\times {10}^{-19}\mathrm{C}$ and Avogadro’s number $=6.023\times {10}^{26}$per kg-atom.

A current of $30$ ampere is flowing through a wire of cross‐sectional area $2 {\mathrm{mm}}^2$. Calculate the drift velocity of electrons. Assuming the temperature of the wire to be $27°\mathrm{C}$, also calculate the $rms$ velocity at this temperature. Which velocity is larger? Given that Boltzmann’s constant $=1.38\times {10}^{-23}{\mathrm{JK}}^{-1}$, density of copper $8.9 \mathrm{g} {\mathrm{cm}}^{-3}$, atomic mass of copper $=63$.

A $10 \mathrm{C}$ of charge flows through a wire in $5$ minutes. The radius of the wire is $1 \mathrm{mm}$. It contains $5\times {10}^{22}$ electrons per ${\mathrm{centimetre}}^3$. Calculate the current and drift velocity.

A current of $2 \mathrm{A}$ is flowing through a wire of length $4 \mathrm{m}$ and cross-sectional area $1 {\mathrm{mm}}^2$. If each cubic metre of the wire contains ${10}^{29}$ free electrons, find the average time taken by an electron to cross the length of the wire.

A copper wire of diameter $1.0 \mathrm{mm}$ carries a current of $0.2 \mathrm{A}$. Copper has $8.4\times {10}^{28}$ atoms per cubic metre. Find the drift velocity of electrons, assuming that one charge carrier of $1.6\times {10}^{-19}\mathrm{C}$ is associated with each atom of the metal.