Equipotential Surfaces and Their Properties

Obtain an expression for the work done to dissociate the system of three charges placed at the vertices of an equilateral triangle of side $‘a’$ as shown here.

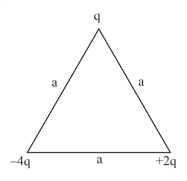
Explain why, for any charge configuration, the equipotential surface through a point is normal to the electric field at that point.

Draw a sketch of equipotential surfaces due to a single charge $\left(-q\right)$, depicting the electric field lines due to the charge.

Sketch equipotential surfaces for a negative point charge.

Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.

Define an equipotential surface. Draw equipotential surfaces Can electric field exist tangential to an equipotential surface? Give reason.

Define an equipotential surface. Draw equipotential surfaces in a constant electric field in $Z$-direction. Why the equipotential surfaces about a single charge are not equidistant?

Define an equipotential surface. Draw equipotential surfaces in the case of a single point charge.

Sketch equipotential surfaces for a uniform electric field.

Sketch equipotential surfaces for two equal and positive charges separated by a small distance.

Sketch equipotential surfaces for two equal and opposite charges separated by a small distance.

Sketch equipotential surfaces for a positive point charges.

Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the region of weak field.

Show that the direction of the electric field is normal to the equipotential surface at every point.

Show that the amount of work done in moving a test charge over an equipotential surface is zero.

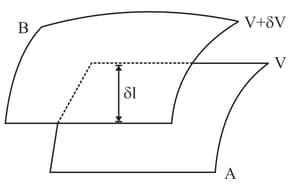
Two closely spaced equipotential surfaces $A$ and $B$ with potentials $V$ and $V+\delta V$, (where $\delta V$ is the change in $V$), are kept $\delta l$ distance apart as shown in the figure. Deduce the relation between the electric field and the potential gradient between them. Write the two important conclusions concerning the relation between the electric field and electric potentials.

Two charges $2 \mu C$ and $-2 \mu C$ are placed at points $A$ and $B, 5 \mathrm{cm}$ apart. Depict an equipotential surface of the system.

A charge $Q$ is distributed over two concentric hollow spheres of radii $r$ and $R$, where $R>r$, such that the surface charge densities are equal. Find the potential at the common centre.

Draw $3$ equipotential surfaces corresponding to a field that uniformly increases in magnitude but remains constant along $Z$-direction. How are these surfaces different from that of a constant electric field along $Z$-direction?

Does the charge given to a metallic sphere depend on whether it is hollow or solid? Give reason for your answer.

No work is done in moving a test charge over an equipotential surface. Why?