Pre-RMO 2015

The digits of a positive integer $n$ are four consecutive integers in decreasing order when read from left to right. If the sum of the possible remainders when $n$ is divided by $37$ is $k$, then the sum of digits of $k$ is 

The circle $\omega$ touches the circle $\Omega$ internally at $P$. The centre $O$ of $\Omega$ is outside $\omega$. Let $XY$ be a diameter of $\Omega$ which is also tangent to $\omega$. Assume $PY>PX$. Let PY intersect $\omega$ at $Z$. If $YZ=2PZ$, what is the magnitude of $\angle PYX$ in degrees?

Let $a, b$ and $c$ be such that $a+b+c=0$ and $P=\frac{a^2}{2a^2+bc}+\frac{b^2}{2b^2+ca}+\frac{c^2}{2c^2+ab}$ is defined. What is the value of $P$?

A subset $B$ of the set of first $100$ positive integers has the property that no two elements of $B$ sum to $125 .$ What is the maximum possible number of elements in B?

In acute-angled triangle $ABC,$ let $D$ be the foot of the altitude from $A$ and $E$ be the midpoint of $BC.$ Let $F$ be the midpoint of $AC.$ Suppose $\angle BAE=40°.$ If $\angle DAE=\angle DFE,$ what is the magnitude of $\angle ADF$ in degrees?

If $3^x+2^y=985$ and $3^x-2^y=473,$ what is the value of $x y$ ?

At a party, each man danced with exactly four women and each woman danced with exactly three men. Nine men attended the party. How many women attended the party?

Let $n$ be the largest integer that is the product of exactly $3$ distinct prime numbers, $x, y$ and $10 x+y,$ where $x$ and $y$ are digits. What is the sum of the digits of $n ?$

Let $a, b,$ and $c$ be real numbers such that $a-7 b+8 c=4$ and $8 a+4 b-c=7.$ What is the value of $a^2-b^2+c^2?$

In rectangle $ABCD, AB=8$ and $BC=20.$ Let $P$ be a point on $AD$ such that $\angle BPC=90°.$ If $r_1, r_2\mathit{ }\text{and} r_3$ are the radii of the incircles of triangles $APB, BPC$ and $CPD,$ what is the value of $r_1+r_2+r_3?$

What is the greatest possible perimeter of a right-angled triangle with integer side lengths if one of the sides has length $12 ?$

A  $2\times 3$ rectangle and a $3\times 4$ rectangle are contained within a square without overlapping at any interior point, and the sides of the square are parallel to the sides of the two given rectangles. What is the smallest possible area of the square?

The figure below shows a broken piece of a circular plate made of glass.

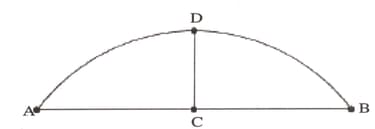
$C$ is the midpoint of $AB$ and $D$ is the midpoint of arc $AB.$ Given that $AB=24 \mathrm{cm}$ and $CD=6 \mathrm{cm}$, what is the radius of the plate in centimetres? (The figure is not drawn to scale)

How many two-digit positive integers $N$ have the property that the sum of $N$ and the number obtained by reversing the order of the digits of $N$ is a perfect square?

Let $E\left(n\right)$ denote the sum of the even digits of $n.$ For example, $E\left(1243\right)=2+4=6.$ What is the value of $\frac{E\left(1\right)+E\left(2\right)+E\left(3\right)+\dots \dots .+E\left(100\right)}{100}$?

How many line segments have both their endpoints located at the vertices of a given cube?

Let $P\left(x\right)$ be a non-zero polynomial with integer coefficients. If $P\left(n\right)$ is divisible by $n$ for each positive integer $n,$ what is the value of $P\left(0\right)$?

The equations $x^2-4x+k=0$ and $x^2+kx-4=0,$ where $k$ is a real number, have exactly one common root. What is the value of $k$?

Positive integers $a$ and $b$ are such that $a+b=\frac{a}{b}+\frac{b}{a}$. What is the value of $a^2+b^2$?

A man walks a certain distance and rides back in $3\frac{3}{4}$ hours; he could ride both ways in $2\frac{1}{2}$ hours. How many hours would it take him to walk both ways?