The Midpoint Theorem of Triangle
Important Questions on The Midpoint Theorem of Triangle
is a triangle right-angled at . A line through the midpoint of hypotenuse and Parallel to intersects at . Show that
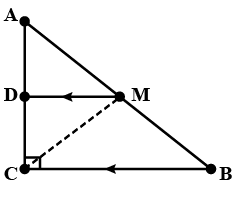
is a triangle right-angled at . A line through the midpoint of hypotenuse and Parallel to intersects at . Show that .
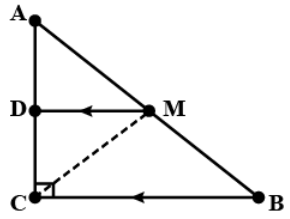
is a triangle right-angled at . A line through the midpoint of hypotenuse and Parallel to intersects at . Show that is the midpoint of
Show that the line segments joining the midpoints of the opposite sides of a quadrilateral and bisect each other.
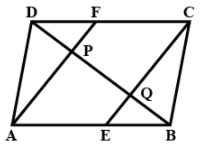
In a parallelogram and are the midpoints of the sides and respectively. Show that the line segment and trisect the diagonal .
Show that the figure formed by joining the midpoints of sides of a rhombus successively is a rectangle.
is quadrilateral and are the midpoints of and respectively. Prove that is a parallelogram.
is a triangle. is a point on such that and is the point on such that . If find .

