Pythagoras Theorem
Important Questions on Pythagoras Theorem
For a right angle triangle with integer sides at least one of its measurements must be an even number. Why?
In a right triangle right-angled at . and are points on sides and respectively which divide these sides in the ratio of .
Prove that .
In a right triangle right-angled at . and are points on sides and respectively which divide these sides in the ratio of .
Prove that .
In a right triangle right-angled at . and are points on sides and respectively which divide these sides in the ratio of .
Prove that
An aeroplane leaves an airport and flies due north at a speed of . At the same time another aeroplane leaves the same airport and flies due west at a speed of . How far apart will the two planes be after hours?
is an isosceles triangle right angle at . Prove that .
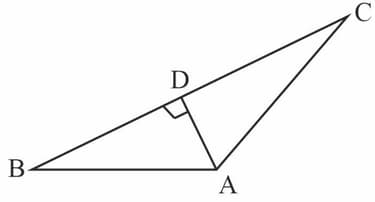
is a triangle right angle at and . Show that .
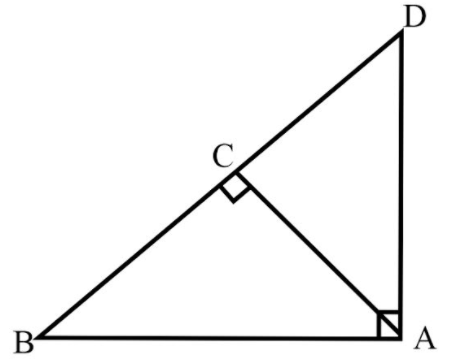
is a triangle right angle at and . Show that .
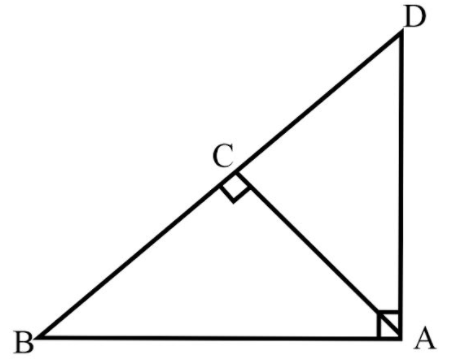
is a triangle right angle at and . Show that .
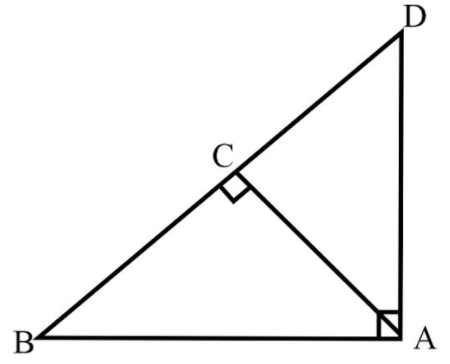
is a triangle right angle at and is a point on such that . Show that .
is an isosceles triangle right-angled at . Equilateral triangles and are constructed on sides and . Find the ratio between the areas of and .
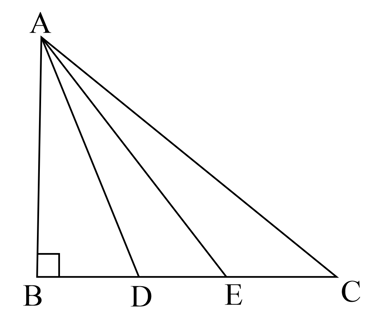
In the given figure, is a triangle right-angled at . and are points on trisect it. Prove that .
In an equilateral triangle, is a point on side such that . Prove that .
Prove that three times the square of any side of an equilateral triangle is equal to four times the square of the altitude.
Two poles of heights and stand on a plane ground. If the distance between the feet of the poles is , find the distance between their tops in meters.
is aright triangle right-angled at . Let and be any points on and respectively. Prove that .
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
A wire attached to vertical pole of height is long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
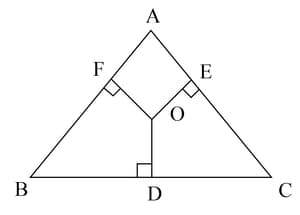
In figure, is any point in the interior of . If and , show that .