O P Malhotra, S K Gupta and, Anubhuti Gangal Solutions for Exercise 1: Exercise
O P Malhotra Mathematics Solutions for Exercise - O P Malhotra, S K Gupta and, Anubhuti Gangal Solutions for Exercise 1: Exercise
Attempt the practice questions from Exercise 1: Exercise with hints and solutions to strengthen your understanding. ICSE Mathematics solutions are prepared by Experienced Embibe Experts.
Questions from O P Malhotra, S K Gupta and, Anubhuti Gangal Solutions for Exercise 1: Exercise with Hints & Solutions
Construct a parallelogram and parallelogram , where and the altitude of each parallelogram is .
In figure, and is parallel to . Name a triangle equal to and a triangle equal in area to , giving your reason. Hence prove that areas of and the quadrilateral are equal.
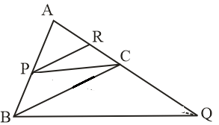
is a parallelogram and is any point on . If is produced meets produced at , prove that the area of triangle area of .
is a parallelogram and is any point on . If is produced meets produced at , prove that the area of triangle area of triangle.
Prove that the parallelogram formed by joining the midpoints of the adjacent sides of a quadrilateral is half of the latter.
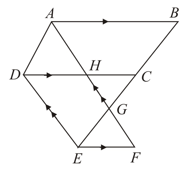
In figure, and . Prove that the area of is equal to the area of .
In the given figure,and are the midpoints of the sides and of the parallelogram and area of the parallelogram is .
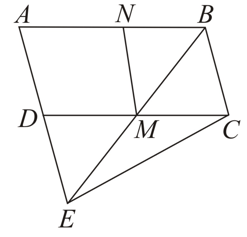
If the area of the triangle is then find the value of .
In the given figure,and are the midpoints of the sides and of the parallelogram and area of the parallelogram is .
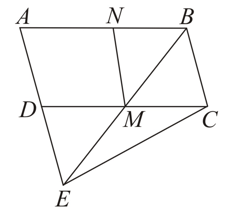
Name the parallelogram which is equal in area to the triangle .
