O P Malhotra, S K Gupta and, Anubhuti Gangal Solutions for Exercise 4: Exercise

The area of a trapezium is $475 {\mathrm{cm}}^2$ and the height is $19 \mathrm{cm}$. Find its two parallel sides if one side is $4 \mathrm{cm}$ greater than the other.

The parallel sides of a trapezium are in the ratio $2 : 5$ and the distance between the parallel sides is $10 \mathrm{cm}$. If the area of the trapezium is $350 {\mathrm{cm}}^2$, find the lengths of its parallel sides.

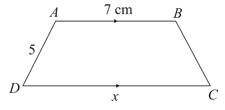
In the given figure, $\mathrm{AD}=\mathrm{BC}=5 \mathrm{cm}, \mathrm{AB}=7 \mathrm{cm}$ The parallel sides $\mathrm{AB}, \mathrm{DC}$ are $4 \mathrm{cm}$ apart. $\mathrm{DC}=\mathrm{x} \mathrm{cm}$. Find $x$ and the area of the trapezium $\mathrm{ABCD}$. 

The parallel sides of a trapezium are $7.5 \mathrm{cm}, 3.9 \mathrm{cm}$; and the other sides are each $2.6 \mathrm{cm}$. Find its area.

The cross-section of a tunnel perpendicular to its length is a trapezium $\mathrm{ABCD}$ as shown in the figure $\mathrm{AM}=\mathrm{BN}; \mathrm{AB}=4.4 \mathrm{m}; \mathrm{CD}=3 \mathrm{m}$. The height of the tunnel is $2.4 \mathrm{m}$. The tunnel is $50 \mathrm{m}$ long.

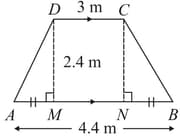
Calculate the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of $₹5 \mathrm{per} {\mathrm{m}}^2.$

The cross-section of a tunnel perpendicular to its length is a trapezium $\mathrm{ABCD}$ as shown in the figure $\mathrm{AM}=\mathrm{BN}, \mathrm{AB}=4.4 \mathrm{m}, \mathrm{CD}=3 \mathrm{m}$. The height of the tunnel is $2.4 \mathrm{m}$. The tunnel is $50 \mathrm{m}$ long.

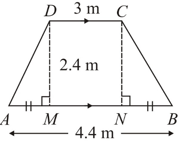
Calculate the cost of paving the floor (in$₹$)at the rate of $₹18 \mathrm{per} {\mathrm{m}}^2$.

A trapezium with its parallel sides in the ratio $11 : 3$ is cut off from a rectangle whose sides measure $98 \mathrm{cm}$ and $12 \mathrm{cm}$. The area of the trapezium is $\frac{3}{7}$ of the area of the rectangle. Find the lengths of the parallel sides of the trapezium, when its height is equal to the smaller side of the rectangle.

The cross-section of a canal is in the shape of a trapezium. If the canal is $12 \mathrm{m}$ wide at the top and $8 \mathrm{m}$ wide at the bottom and the area of its cross-section is $84 {\mathrm{m}}^2$, determine its depth.