Electric Flux

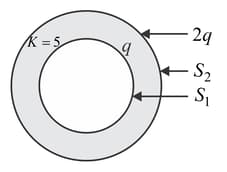
${\mathrm{S}}_1$ and ${\mathrm{S}}_2$ are two hollow concentric spheres with charge $q$ and $2q.$ Space between ${\mathrm{S}}_1$ and ${\mathrm{S}}_2$ is filled with a dielectric of dielectric constant, $K=5$. The ratio of flux through $S_2$ and flux through $S_1$ is $K\text{'}.$ Then find the value of $15K\text{'}.$

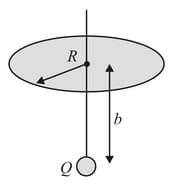
A point charge $Q$ is located on the axis of disc of radius $R$ at a distance $b$ from the plane of the disk. If one fourth of the electric flux from the charge passes through the disk, then $R=\sqrt{\square }b$ (as shown in figure). Suitable value for $\square$ can be,

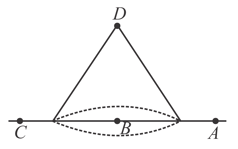
A right circular imaginary cone is shown in the figure. $A, B,$ and $C$ are the points in the plane containing the base of the cone, while $D$ is the point at the vertex of the cone. If ${\mathrm{\varphi }}_{\mathrm{A}}\text{,} {\mathrm{\varphi }}_{\mathrm{B}}\text{,} {\mathrm{\varphi }}_{\mathrm{C}}$ and ${\mathrm{\varphi }}_{\mathrm{D}}$ represent the flux through the curved surface of the cone when a point charge $Q$ is at points $A\text{,} B\text{,} C\text{,}$ and $D$ respectively, then

Two charges $Q_1$ and $Q_2$ lie inside and outside, respectively, of a closed surface $S$. Let $E$ be the field at any point on $S$ and $\varphi$ be the flux of $E$ over $S$.

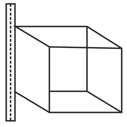
An infinite wire having charge density $\lambda$ passes through one of the edges of a cube having edge length $\text{'}l\text{'}$. Find the

(a) total flux passing through the cube,
(b) flux passing through the surfaces which are in contact with the wire,
(c) flux passing through the surfaces which are not in contact with the wire.

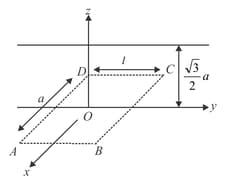
An infinitely long uniform line charge distribution of charge per unit length $\lambda$ lies parallel to the $y$-axis in the $y-z$ plane at $z =\frac{\sqrt{3}}{2}a$ (see figure). If the magnitude of the flux of the electric field through the rectangular surface $ABCD$ lying in the $x-y$ plane with the centre at the origin is $\frac{\lambda l}{n{\epsilon }_0}$ (${\epsilon }_0$ is permittivity of free space ), then the value of $n$ is ____.

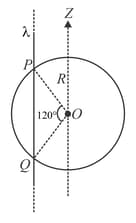
An infinitely long thin non-conducting wire is parallel to the $z$-axis and carries a uniform line charge density $\lambda$. It pierces a thin non-conducting spherical shell of radius $R$ in such a way that the arc $PQ$ subtends an angle $120°$ at the centre $O$ of the spherical shell, as shown in the figure. The permittivity of free space is ${\epsilon }_0$. Which of the following statements (are) true?

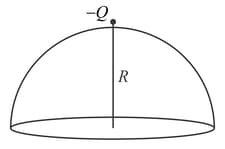
A point charge $+Q$ is placed just outside an imaginary hemispherical surface of radius $R$ as shown in the figure. Which of the following statements is/are correct?

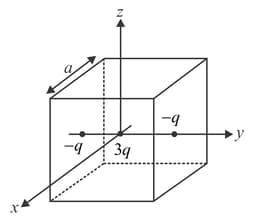
A cubical region of side a has its centre at the origin. It encloses three fixed point charges, $-q$ at $\left(0, -\frac{a}{4}, 0\right), +3q$ at $\left(0, 0, 0\right), -q$ at $\left(0, +a/4, 0\right)$. Choose the correct option(s).

Consider electric field $\overrightarrow{E} = E_0\hat{x}$, where $E_0$ is a constant. The flux through the shaded area (as shown in the figure) due to this field is:

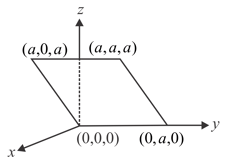
One-fourth of a sphere of radius $R$ is removed as shown in the figure. An electric field $E$ exists parallel to the $xy$ plane. Find the flux through the remaining curved part.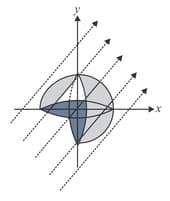

The number of electric field lines crossing an area $∆\overrightarrow{S}$ is $n_1$ when $∆\overrightarrow{S}\left|\right|\overrightarrow{E}$, while the number of field lines crossing the same area is $n_2$ when $∆\overrightarrow{S}$ makes an angle of $30°$ with $\overrightarrow{E}$. Then

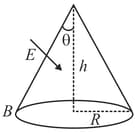
A conic surface is placed in a uniform electric field $E$ as shown in the figure such that the field is perpendicular to the surface on the side $AB$. The base of the cone is of the radius $R$, and the height of the cone is $h$. The angle of the cone is $\mathrm{\theta }$. Find the magnitude of the flux that enters the cone’s curved surface from the left side. Do not count the outgoing flux $\left(\mathrm{\theta }<45°\right)$.

A flat, square surface with sides of length $L$ is described by the equations $x=L$, $0\le y\le L$, $0\le z\le L$. The electric flux through the square due to a positive point charge $q$ located at the origin $\left(x=0, y=0, z=0\right)$ is

In a region of space, the electric field is given by $\overrightarrow{E}=8\hat{\mathrm{i}}+4\hat{\mathrm{j}}+3\hat{\mathrm{k}}$. The electric flux through the surface of the area $100 \mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{s}$ in the $xy$ plane is

A cylinder of the length $L$ and the radius $b$ has its axis coincident with the $x-$axis. The electric field in this region is $\overrightarrow{E}=200\widehat{\mathrm{i}}$. Find the flux through the left end of the cylinder.