Work-energy Theorem

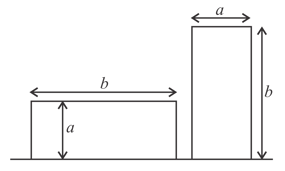
A plate of mass undefined length $b$ and breadth $a$ is initially lying on a horizontal floor with length parallel to the floor and breadth perpendicular to the floor. Find the work done to erect it on its breadth.

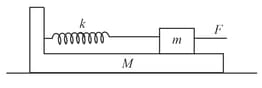
A constant force $F$ pushes the block $m$ till the wedge $M$ starts sliding. If the stiffness of the light spring connecting $M$ and $m$ is $k$, coefficient of friction between block and wedge is ${\mu }_1$, and between the wedge and ground is ${\mu }_2$, then find the value of the force $F$

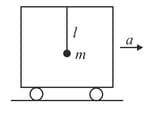
A pendulum of mass $m$ and length $l$ is suspended from the ceiling of a trolley which has a constant acceleration $a$ in the maximum deflection $\mathrm{\theta }$ of the pendulum from the vertical. Find $\mathrm{\theta }$

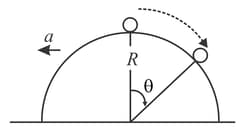
A small ball is placed at the top of a smooth hemispherical wedge of radius $R$. If the wedge is accelerated with an acceleration $a$, find the velocity of the ball relative to the wedge as the function of $\mathrm{\theta }$.

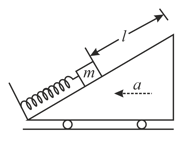
A block of mass $m$ is welded with a light spring of stiffness $k$. The spring is initially relaxed. When the wedge fitted moves with acceleration $a$, as shown in the figure, the block slides through a maximum distance $l$ relative to the wedge. If the coefficient of kinetic friction between the block and the wedge is $\mu$, find the maximum deformation $l$ of the spring by using the work-energy theorem.

A block of mass $m$ is slowly lowered from a point where it just touches a vertical fixed spring of stiffness $k$, till it remains stationary after the applied force is withdrawn. Find the work done by the external agent 

$\left(\mathrm{a}\right)$ in compressing the spring by a distance $x$ and

$\left(\mathrm{b}\right)$ bringing the block to its stable equilibrium position.

A plank of mass $M$ and length $L$ is placed at rest on a smooth horizontal surface. A small block of mass $m$ is projected with a velocity $v_0$ from the left end of it as shown in the figure. The coefficient of friction between the block and the plank is $\mu$, and its value is such that the block becomes stationary with respect to the plank before it reaches the other end.

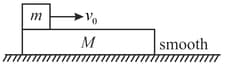
$\left(\mathrm{a}\right)$ Find the time and common velocity when relative sliding between the block and the plank stops.

$\left(\mathrm{b}\right)$ Find the work done by the friction force on the block during the period it slides on the plank. Is the work positive or negative?

$\left(\mathrm{c}\right)$ Calculate the work done on the plank during the same period. Is the work positive or negative?

$\left(\mathrm{d}\right)$ Also, determine the net work done by friction. Is it positive or negative?

Two blocks are connected by a string, as shown in the figure. They are released from rest. Show that after they have moved a distance $L$, their common speed is given by $v=\sqrt{2\left(m_2-\mu m_1\right)gL/\left(m_1+m_2\right)}$, which $\mu$ is the coefficient of kinetic friction between the upper block and the surface. Assume that the pulley is massless and frictionless.

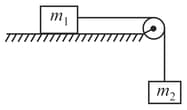
Consider an elliptically shaped rail $PQ$ in the vertical plane with $OP=3 \mathrm{m}$ and $OQ=4 \mathrm{m}.$ A block of mass $1 \mathrm{kg}$ is pulled along the rail from $P$ to $Q$ with a force of $18 \mathrm{N},$ which is always parallel to line $PQ$ (see the figure given). Assuming no frictional losses, the kinetic energy of the block when it reaches $Q$ is $(n\times 10) \mathrm{joules}$ . The value of $\mathrm{n}$ is (take acceleration due to gravity $=10{ \mathrm{ms}}^{-2}$)

A particle of mass $0.2 \mathrm{kg}$ is moving in one dimension under a force that delivers a constant power $0.5 \mathrm{W}$ to the particle. If the initial speed (in $\mathrm{m} {\mathrm{s}}^{-1}$) of the particle is zero, the speed (in $\mathrm{m} {\mathrm{s}}^{-1}$) after $5 \mathrm{s}$ is

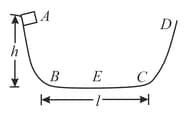
A particle slides along a track with elevated ends and a flat central part as shown in the figure. The flat part has a length $l=3 \mathrm{m}$. The curved portions of the track are frictionless. For the flat part, the coefficient of kinetic friction is ${\mu }_{\mathrm{K}}=0.2$. The particle is released at the point $A$ which is at height $h=1.5 \mathrm{m}$ above the flat part of the track. Where does the particle finally come to rest?

A block of mass $m$ is moving with an initial velocity $v_{\circ }$ towards a stationary spring of stiffness $k$ attached to the wall as shown in figure.

(a) Find the maximum compression in the spring. 

(b) Is the work done by the spring negative or positive?

A bullet leaving the muzzle of a rifle barrel with a velocity $v$ penetrates a plank and loses one-fifth of its velocity. It then strikes second plank, which it just penetrates through. Find the ratio of the thickness of the planks, supposing the average resistance to the penetration is same in both the cases.

A time dependent force, $F=6t$ acts on a particle of mass $1 \mathrm{kg}$. If the particle starts from rest, the work done by the force during the first $1 \sec$ will be,

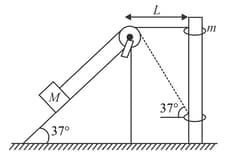
A ring of mass $m=1\mathrm{kg}$ can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of $L=0.7 \mathrm{m}$ from the rod is shown in the figure. At the other end of the string, mass $M=5\mathrm{kg}$ is attached, lying over a smooth fixed inclined plane of inclination angle $37°$. The ring is held in level with the pulley and released. Determine the velocity of ring $\left(\mathrm{in} \mathrm{m} {\mathrm{s}}^{-1}\right)$ when the string makes an angle $\left(\alpha =37°\right)$ with the horizontal, $\left[\sin 37°=0.6\right]$

Two blocks having masses $8 \mathrm{kg}$ and $16 \mathrm{kg}$ are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible string also connects $B$ with ceiling as shown in the figure at the initial moment. Initially, the spring has its natural length. A constant horizontal force $F$ is applied to the heavier block as shown. What is the maximum possible value of $F \text{(in} \mathrm{N}\text{)}$ so the lighter block does not lose contact with ground.

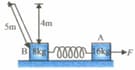
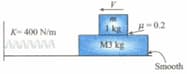
As shown in the figure, there is no friction between the horizontal surface and the lower block $(M=3 \mathrm{kg})$ but the friction coefficient between both the blocks is $0.2$. Both the blocks move together with initial speed $V$ towards the spring, compresses it and due to the force exerted by the spring, moves in the reverse direction of the initial motion. Find the maximum value of $V (\mathrm{in} \mathrm{cm} {\mathrm{s}}^{-1})$ so that during the motion, there is no slipping between the blocks. $(g=10 \mathrm{m} {\mathrm{s}}^{-2})$.

In the figure, the variation of components of acceleration of a particle of mass $1 \mathrm{kg}$ is shown w.r.t. time. The initial velocity of the particle is $\overrightarrow{u}=\left(-3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}\right) \mathrm{m} {\mathrm{s}}^{-1}$. Find the total work done by the resultant force on the particle in the time interval from $t=0$ to $t=4$ seconds in $\mathrm{J}$.

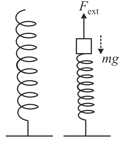
A block of mass $M$ rests on a table. It is fastened to the lower end of a light, vertical spring. The upper end of the spring is fastened to a block of mass $m$. The upper block is pushed down by an additional force $3mg$, so the spring compression is $4 \frac{mg}{k}$. In this configuration, the upper
block is released from rest. The spring lifts the lower block off the table. What is the greatest possible value for $\frac{M}{m}$?

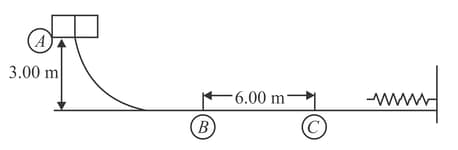
A $10.0-\mathrm{kg}$ block is released from rest at point $\overline{)A}$ in figure. The track is frictionless except for the portion between points $\overline{)B}$ and $\overline{)C}$, which has a length of $6.00 \mathrm{m}$. The block travels down the track, hits a spring of force constant $3000 \mathrm{N} {\mathrm{m}}^{-1}$ and compresses the spring $0.20 \mathrm{m}$ from its equilibrium position before coming to rest momentarily.
If the coefficient of kinetic friction between the block and the rough surface between points $\overline{)B}$ and $\overline{)C}$ is $10 x$. Find the value of $x$.