ADDITIONAL EXERCISES

A square loop of side $12 \mathrm{cm}$ with its sides parallel to $\mathrm{X} \mathrm{and} \mathrm{Y}$ axis is moved with a velocity $8 \mathrm{cm}/\mathrm{s}$ in the positive $x-$direction in an environment containing magnetic field in the positive $z-$direction. The field is neither uniform in space or constant in time. It has a gradient of ${10}^{-3} \mathrm{T} {\mathrm{cm}}^{-1}$ in the negative $\mathrm{x}-$direction( i.e. it increases by ${10}^{-3} \mathrm{T} {\mathrm{cm}}^{-1}$ as one moves along the -ve $\mathrm{x}-$direction) and it is decreasing in time at the rate of ${10}^{-3} {\mathrm{Ts}}^{-1}$. Determine the direction and magnitude of the induced current in the loop if its resistance is $4.5 \mathrm{m\Omega }$.

It is desired to measure the magnitude of field between the poles of a powerful loudspeaker magnet. A small flat search coil of area $2 {\mathrm{cm}}^2$ with $25$ closely wound turns, is positioned normal to the field direction, and then quickly snatched out of the region. Equivalently, one can give it a quick ${90}^{°}$ turn to bring its plane parallel to the field direction. The total charge flown in coil ( measured by ballistic galvanometer connected to the coil) is $7.5 \mathrm{mC}$. The combined resistance of coil and galvanometer is $0.50 \mathrm{\Omega }$. Calculate the field strength of the magnet.

Figure below shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutually perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod $=15 \mathrm{c}\mathrm{m}$, $B=0.50 \mathrm{T}$, resistance of the closed loop containing the rod $=9.0 \mathrm{m}\mathrm{\Omega }$. Assume the field to be uniform.

With K open and the rod is moved with a velocity $12 \mathrm{cm}/\mathrm{s}$ in the direction shown. Give the polarity and magnitude of induced emf.

Figure below shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutually perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod $=15 \mathrm{c}\mathrm{m}$, $B=0.50 \mathrm{T}$, resistance of the closed loop containing the rod $=9.0 \mathrm{m}\mathrm{\Omega }$. Assume the field to be uniform.

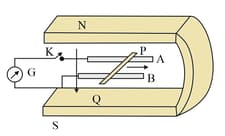
Is there an excess charge built up at the ends of the rod when K is open? What if K is closed?

Figure below shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutually perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod $=15 \mathrm{c}\mathrm{m}$, $B=0.50 \mathrm{T}$, resistance of the closed loop containing the rod $=9.0 \mathrm{m}\mathrm{\Omega }$. Assume the field to be uniform. Given that rod is moved with velocity $12 \mathrm{cm}/\mathrm{s}$ in given direction.

What is the retarding force on the rod when K is closed? How much power is required (by an external agent) to keep the rod moving at same speed  $(=12 {\mathrm{cms}}^{-1})$ when K is closed? How much power is required when K is open?

Figure below shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutually perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod $=15 \mathrm{c}\mathrm{m}$, $B=0.50 \mathrm{T}$, resistance of the closed loop containing the rod $=9.0 \mathrm{m}\mathrm{\Omega }$. Assume the field to be uniform.

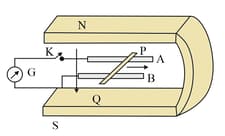
How much power is dissipated as heat in the closed-circuit? What is the source of this power?

Figure below shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutually perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod $=15 \mathrm{c}\mathrm{m}$, $B=0.50 \mathrm{T}$, resistance of the closed loop containing the rod $=9.0 \mathrm{m}\mathrm{\Omega }$. Assume the field to be uniform.

What is the induced emf in the moving the rod if the magnetic field is parallel to the rails instead of being perpendicular?

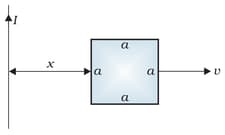
Consider the mutual inductance between a long straight wire and a square loop of side $\mathrm{a}$ as shown in the figure below.
Now assume that the straight wire carries a current of $50 \mathrm{A}$ and the loop is moved to the right with a constant velocity, $v=10 \mathrm{m}/\mathrm{s}$. Calculate the induced emf in the loop at the instant when $x=0.2 \mathrm{m}$. Take $a=0.1 \mathrm{m}$ and assume that the loop has a large resistance.