NCERT Solutions for Chapter: Kinetic Theory, Exercise 1: EXERCISES

Figure below shows plot of $\frac{\mathrm{PV}}{\mathrm{T}}$ versus P for $1.00\times {10}^{–3} \mathrm{kg}$ of oxygen gas at two different temperatures.

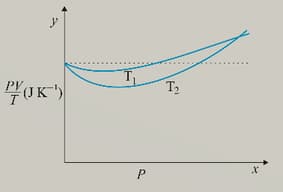
Which is true:$T_1>T_2$ or $T_1<T_2$

Figure below shows plot of $\frac{\mathrm{PV}}{\mathrm{T}}$ versus $\mathrm{P}$ for $1.00\times {10}^{–3} \mathrm{kg}$ of oxygen gas at two different temperatures.

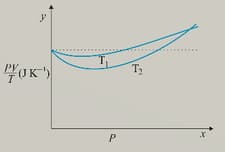
What is the value of $\frac{\mathrm{PV}}{\mathrm{T}}$ where the curves meet on the y-axis?

Figure below shows plot of $\frac{\mathrm{PV}}{\mathrm{T}}$ versus $\mathrm{P}$ for $1.00\times {10}^{–3} \mathrm{kg}$ of oxygen gas at two different temperatures.

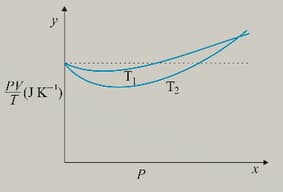
If we obtained similar plots for $1.00\times {10}^{–3} \mathrm{kg}$ of hydrogen, would we get the same value of $\frac{\mathrm{PV}}{\mathrm{T}}$ at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of $\frac{\mathrm{PV}}{\mathrm{T}}$ (for low pressure, high temperature region of the plot)? (Molecular mass of ${\mathrm{H}}_2=2.02 \mathrm{u}$, of ${\mathrm{O}}_2=32.0 \mathrm{u}$, $\mathrm{R}=8.31{\mathrm{Jmol}}^{–1}{\mathrm{K}}^{–1}$
)

Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at $2.0 \mathrm{atm}$ and temperature $17 °\mathrm{C}$. Take the radius of a nitrogen molecule to be roughly $1.0 {\mathrm{A}}^{°}$. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of ${\mathrm{N}}_2 = 28.0 \mathrm{u}$).

A metre long narrow bore held horizontally (and closed at one end) contains a $76 \mathrm{cm}$ long mercury thread, which traps a $15 \mathrm{cm}$ column of air. What happens if the tube is held vertically with the open end at the bottom?

From a certain apparatus, the diffusion rate of hydrogen has an average value of $28.7 {\mathrm{cm}}^3{\mathrm{s}}^{–1}$. The diffusion of another gas under the same conditions is measured to have an average rate of $7.2 {\mathrm{cm}}^3{\mathrm{s}}^{–1}$. Identify the gas. [Hint: Use Graham’s law of diffusion: $R_1/R_2={\left(\frac{M_2}{M_1}\right)}^{1/2},$ where $R_1,R_2$ are diffusion rates of gases 1 and 2, and $M_1$ and $M_2$ their respective molecular masses. The law is a simple consequence of kinetic theory.]

A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so-called law of atmospheres

${\mathrm{n}}_2={\mathrm{n}}_1\exp \left[-\mathrm{mg}\left({\mathrm{h}}_2-{\mathrm{h}}_1\right)/{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\right]$
where ${\mathrm{n}}_2, {\mathrm{n}}_1$ refer to number density at heights ${\mathrm{h}}_2$ and ${\mathrm{h}}_1$ respectively. Use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid column:
${\mathrm{n}}_2={\mathrm{n}}_1\exp \left[-{\mathrm{mgN}}_{\mathrm{A}}\left(\mathrm{\rho }-\mathrm{\rho }\text{'}\right)\left({\mathrm{h}}_2-{\mathrm{h}}_1\right)/\left(\mathrm{\rho RT}\right)\right]$
where $\mathrm{\rho }$ is the density of the suspended particle, and $\mathrm{\rho }\text{'}$ that of the surrounding medium.
[ ${\mathrm{N}}_{\mathrm{A}}$ is Avogadro’s number, and $\mathrm{R}$ the universal gas constant.]

Given below are densities of some solids and liquids. Give rough estimates of the size of their atoms:

[Hint: Assume the atoms to be ‘tightly packed’ in a solid or liquid phase, and use the known value of Avogadro’s number. You should, however, not take the actual numbers you obtain for various atomic sizes too literally. Because of the crudeness of the tight packing approximation, the results only indicate that atomic sizes are in the range of a few $\AA$].