Velocity and Acceleration in Simple Harmonic Motion

A body describes simple harmonic motion with an amplitude of $5 \mathrm{cm}$ and a period of $0.2 \mathrm{s}.$ Find the acceleration and velocity of the body when the displacement is  $0 \mathrm{cm}.$

A body describes simple harmonic motion with an amplitude of $5 \mathrm{cm}$ and a period of $0.2 \mathrm{s}.$ Find the acceleration and velocity of the body when the displacement is $3 \mathrm{cm}$.

What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity? 

A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall? 

The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than $2\pi \sqrt{\frac{l}{g}}$. Think of a qualitative argument to appreciate this result.

In Exercise $14.9$, let us take the position of mass when the spring is unstretched as $\mathrm{x} = 0$, and the direction from left to right as the positive direction of$\mathrm{x}-$axis. Give x as a function of time $\mathrm{t}$ for the oscillating mass if at the moment we start the stopwatch $(\mathrm{t} = 0)$, the mass is at the maximum compressed position.In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?

In Exercise $14.9$, let us take the position of mass when the spring is unstretched as $\mathrm{x} = 0$, and the direction from left to right as the positive direction of$\mathrm{x}-$axis. Give x as a function of time $\mathrm{t}$ for the oscillating mass if at the moment we start the stopwatch $(\mathrm{t} = 0)$, the mass is at the maximum stretched position, and In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?

A spring having with a spring constant $1200 \mathrm{N} {\mathrm{m}}^{-1}$ is mounted on a horizontal table as shown. A mass of $3 \mathrm{kg}$ is attached to the free end of the spring. The mass is then pulled sideways to a distance of$2.0 \mathrm{cm}$ and released.

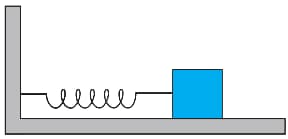
Determine the maximum speed of the mass.

A spring having with a spring constant $1200 \mathrm{N} {\mathrm{m}}^{-1}$ is mounted on a horizontal table as shown. A mass of $3 \mathrm{kg}$ is attached to the free end of the spring. The mass is then pulled sideways to a distance of$2.0 \mathrm{cm}$ and released.

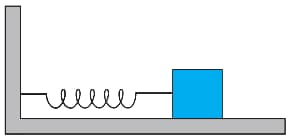
Determine maximum acceleration of the mass.

The motion of a particle executing simple harmonic motion is described by the displacement function,
$\mathrm{x}\left(\mathrm{t}\right)=\mathrm{A} \cos \left(\mathrm{\omega t}+\mathrm{\varphi }\right)$
If the initial $(\mathrm{t} = 0)$ position of the particle is $1 \mathrm{cm}$and its initial velocity is $\mathrm{\omega } \mathrm{cm}/\mathrm{s}$, what are its amplitude and initial phase angle? The angular frequency of the particle is$\mathrm{\pi } {\mathrm{s}}^{-1}$. If instead of the cosine function, we choose the sine function to describe the SHM: $\mathrm{x}\left(\mathrm{t}\right)=\mathrm{A} \sin \left(\mathrm{\omega t}+\mathrm{\varphi }\right)$, what are the amplitude and initial phase of the particle with the above initial conditions.

A particle is in linear simple harmonic motion between two points, $\mathrm{A}$ and $\mathrm{B}$, $10 \mathrm{cm}$apart. Take the direction from $\mathrm{A}$ to $\mathrm{B}$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at $4 \mathrm{cm}$ away $\mathrm{B}$ going towards $\mathrm{B}$.

A particle is in linear simple harmonic motion between two points, $\mathrm{A}$ and $\mathrm{B}$, $10 \mathrm{cm}$apart. Take the direction from $\mathrm{A}$ to $\mathrm{B}$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is  at $3 \mathrm{cm}$ away from $\mathrm{A}$ going towards $\mathrm{B}$.

A particle is in linear simple harmonic motion between two points, $\mathrm{A}$ and $\mathrm{B}$, $10 \mathrm{cm}$apart. Take the direction from $\text{A}$ to $\mathrm{B}$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at $2 \mathrm{cm}$ away from $\mathrm{B}$ going towards $\mathrm{A}$.

A particle is in linear simple harmonic motion between two points, $\mathrm{A}$ and $\mathrm{B}$, $10 \mathrm{cm}$apart. Take the direction from $\mathrm{A}$ to $\mathrm{B}$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at the midpoint of $\mathrm{AB}$ going towards A.

A particle is in linear simple harmonic motion between two points, $\mathrm{A}$ and $\mathrm{B}$, $10 \mathrm{cm}$apart. Take the direction from $\mathrm{A}$ to $\mathrm{B}$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is at the end $\mathrm{B}$.

A body describes simple harmonic motion with an amplitude of $5 \mathrm{cm}$ and a period of $0.2 \mathrm{s}.$ Find the acceleration and velocity of the body when the displacement is$5 \mathrm{cm}$.

Time period of a particle in SHM depends on the force constant $\mathrm{k}$ and mass $\mathrm{m}$ of the particle:
$\mathrm{T}=2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$. A simple pendulum executes SHM approximately. Why then is the time period of a pendulum independent of the mass of the pendulum?

The acceleration due to gravity on the surface of moon is $1.7 {\mathrm{ms}}^{-2}$. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is $3.5 \mathrm{s}$? ($\mathrm{g}$ on the surface of earth is $9.8 {\mathrm{ms}}^{-2}$)

The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of $1 \mathrm{m}$. If the piston moves with simple harmonic motion with an angular frequency of $200 \mathrm{rad}/\min$, what is its maximum speed?

A spring having with a spring constant $1200 \mathrm{N} {\mathrm{m}}^{-1}$ is mounted on a horizontal table as shown. A mass of $3 \mathrm{kg}$ is attached to the free end of the spring. The mass is then pulled sideways to a distance of$4.0 \mathrm{cm}$ and released. Let us take the position of mass when the spring is unstretched as $\mathrm{x} = 0$, and the direction from left to right as the positive direction of$\mathrm{x}-$axis. Give $\mathrm{x}$ as a function of time $\mathrm{t}$ for the oscillating mass if at the moment we start the stopwatch $(\mathrm{t} = 0)$, the mass is
a) at the mean position.
b) at the maximum stretched position
c) at the maximum compressed position

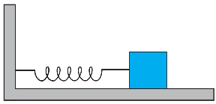
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?