Kinetic Energy of Rotating Body About a Fixed Axis

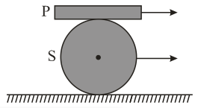
A plank $P$ is placed on a solid cylinder $S$, which rolls on a horizontal surface. The two are of equal mass. There is no slipping at any of the surfaces in contact. The ratio of the kinetic energy of $P$ to the kinetic energy of $S$ is

A constant external torque $\tau$ acts for a very brief period $∆t$
on a rotating system having moment of inertia $I$ , then

A rod of mass $m$ spins with an angular speed $\omega =\sqrt{g/l}$ , Find its

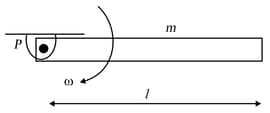
(a) kinetic energy of rotation.
(b) kinetic energy of translation
(c) total kinetic energy.

A ring of mass $3 \mathrm{kg}$ is rolling without slipping with linear velocity $1{ \mathrm{ms}}^{-1}$ on a smooth horizontal surface. A rod of same mass is fitted along its one diameter. Find total kinetic energy of the system (in $J$).

A solid sphere rolls on a smooth horizontal surface at $10 \mathrm{m}/\mathrm{s}$ and then rolls up a smooth inclined plane of inclination $30°$ with horizontal. The mass of the sphere is $2 \mathrm{kg}$. Find the height attained by the sphere before it stops (in $m$ ).

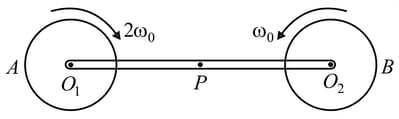
A rod of mass '$M$' and length $6 R$ is pivoted at its centre (point $P$) to rotate in vertical plane as shown. Two discs of same radius $\text{'}R\text{'}$ are joined at the ends $O,$ and $O_2$ of the rod. Mass of the discs $A$ and $B$ are $\text{'}M$ and $\text{'}2M\text{'}$ respectively. Initial angular velocities of discs are shown in figure. The system is released from rest from horizontal position. Find the angular velocity of the $\mathit{rod}$ (in $\mathrm{rad} {\sec }^{-1}$)when it is vertical. (Given $R=0.5 \mathrm{m}$ and $g=10 {\mathrm{ms}}^{-2}$)

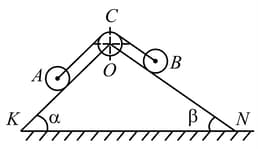
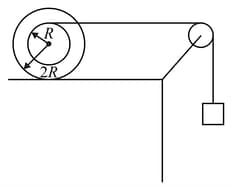
A wheel $\mathrm{A}$ is connected to a second wheel $\mathrm{B}$ by means of inextensible string, passing over a pulley $\mathrm{C}$, which rotates about a fixed horizontal axle $\mathrm{O}$, as shown in the figure. The system is released from rest. The wheel $\mathrm{A}$ rolls down the inclined plane $\mathrm{OK}$ thus pulling up wheel $\mathrm{B}$ which rolls along the inclined plane $\mathrm{ON}$ Determine the velocity (in $\mathrm{m}/\mathrm{s}$ ) of the axle of wheel $\mathrm{A}$, when it has travelled a distance $s=3.5 \mathrm{m}$ down the slope. Both wheels and the pulley are assumed to be homogeneous disks of identical weight and radius. Neglect the weight of the string. The string does not slip over $\mathrm{C}$. [Take $\alpha =53°$ and $\beta =37°$ ]

In the previous problem the normal force between the ball and the shell in position $B$ is

In the figure shown mass of both, the spherical body and block is $m$. Moment of inertia of the spherical body about centre of mass is $2m{R}^2$. The spherical body rolls on the horizontal surface. There is no slipping at any surfaces in contact. The ratio of kinetic energy of the spherical body to that of block is

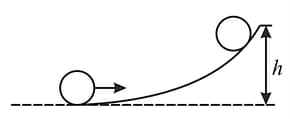
In the figure shown, a ball without sliding on a horizontal surface. It ascends a curved track up to height $h$ and returns. The value of $h$ is $h$ for sufficiently rough curved track to avoid sliding and is $h_2$ for smooth curved track, then

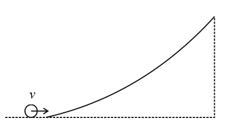
A body is rolling without slipping on a horizontal plane. The rotational energy of the body is $40\%$ of the total kinetic energy. Identify the body.

A small object of uniform density rolls up a curved surface with an initial velocity $v$. It reaches up to a maximum height of $\frac{3v^2}{4g}$ with respect to the initial position. The object is 

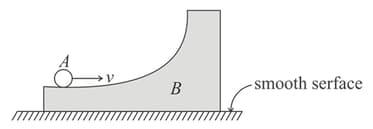
In the figure shown a ring $A$ is rolling without sliding with a velocity $v$ on the horizontal surface of the body $B$ (of the same mass as $A$). All surfaces are smooth. $B$ has no initial velocity. What will be the maximum height (from initial position) reached by $A$ on $B$.

A rigid body is made of three identical uniform thin rods each of length $L$ fastened together in the form of letter $H.$The body is free to rotate about a fixed horizontal axis $\mathrm{AB}$that passes through one of the legs of the$H.$ The body is allowed to fall from rest from a position in which the plane of $H$ is horizontal. What is the angular speed of the body, when the plane of $H$ is vertical. 

A loop and a disc roll, without slipping, with same linear velocity $v$. The mass of the loop and the disc is same. If the total kinetic energy of the loop is $8 \mathrm{J}$, find the kinetic energy of the disc (in $\mathrm{J}$).

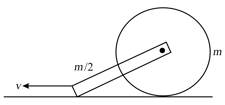
A uniform disc of mass $m$ is fitted (pivoted smoothly) with a rod of mass $m/2$ . If the bottom of the rod is pulled with a velocity $v$ , it moves without changing its angle of orientation and the disc rolls without sliding. Find the kinetic energy of the system $(\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{}+\mathrm{}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c})$ .

A copper ball of mass $m=1 \mathrm{k}\mathrm{g}$ with a radius of $r=10 \mathrm{c}\mathrm{m}$ rotates with angular velocity $\mathrm{\omega }=2 \mathrm{rad} {\mathrm{s}}^{-1}$ about an axis passing through its centre. What work should be performed to increase the angular velocity of rotation of the ball two-fold?

A solid uniform disc of mass $m$ and radius $R$ is pivoted about a horizontal axis through its centre and a small body of mass $m$ is attached to the rim of the disk. If the disc is released from rest with the small body, initially at the same level as the centre, find the angular velocity when the small body reaches the lowest point of the disk.

A uniform rod of length $l$ is released from rest such that it rotates about a smooth pivot. Find the angular speed of the rod when it becomes vertical.

A uniform rod of mass $m$ and length $l$ is kept vertical with the lower end clamped. It is slightly pushed to let it fall down under gravity. Find its angular speed when the rod is passing through its lowest position. Neglect any friction at the clamp. What will be the linear speed of the free end at this instant?