Faraday's Law of Electromagnetic Induction

(b) A circular coil of diameter $200mm$ has $600$ turns is shown. It is placed with its plane perpendicular to a horizontal magnetic field of uniform flux density $50mT.$. The coil is then rotated through $90°$ about a vertical axis in a time of$120ms$

(iii) the average magnitude of the induced e.m.f. in the coil during the rotation.

(a) State Faraday's law of electromagnetic induction.

This diagram shows a square coil about to enter a region of uniform magnetic field of magnetic flux density $0.30T.$ The magnetic field is at right angles to the plane of the coil. The coil has $150$ turns and each side is$2.0cm$ in length. The coil moves at a constant speed of $0.50m{s}^{-1}$

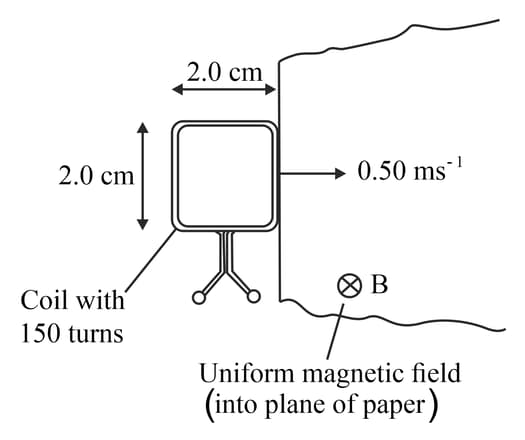
(c) Determine the induced e.m.f. across the ends of the coil. 

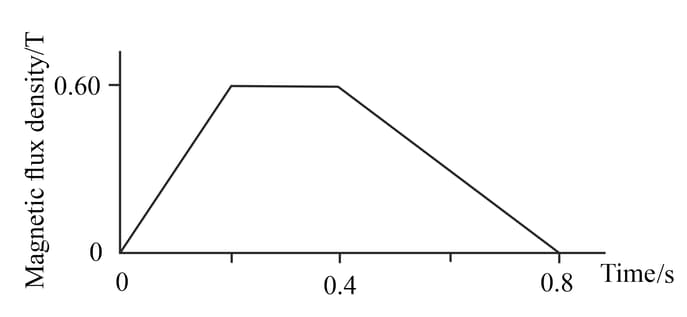
(6) (b) This is a graph of magnetic flux density through a $240$ turn coil with a cross-sectional area $1.2\times {10}^{-4}{m}^2$ against time. 

(iii) Sketch a diagram to show the induced e.m.f. varies with time. Mark values on both the $e.m.f.$ and time axes.

(6) (b) This is a graph of magnetic flux density through a $240$ turn coil with a cross-sectional area $1.2\times {10}^{-4}{m}^2$ against time. 

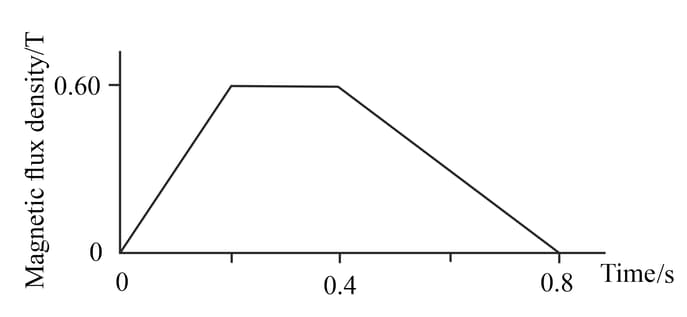
(ii) Determine the maximum magnitude of the induced e.m.f. in the coil.

An aircraft of wingspan $40m$ flies horizontally at a speed of$300\pm 10m{s}^{-1}$ in a region where the vertical component of the Earth's magnetic field is $5.0\times {10}^{-5}T.$

Calculate the magnitude of the e.m.f. induced between the aircraft's wing tips; in your answer, include the absolute uncertainty.

A square coil of $100$ turns of wire has sides of length $5.0 cm.$ It is placed in a magnetic field of flux density $20 mT,$ so that the flux is perpendicular to the plane of the coil

(b) The coil is now pulled from the magnetic field in a time of $0.10s.$Calculate the average $e.m.f.$ induced in it.

A student thinks that electrical current passes through the core in a transformer to the secondary coil. Describe how you might demonstrate that this is not true and explain how an electrical current is actually induced in the secondary coil. Use Faraday's law in your explanation.

The peak e.m.f. induced in a rotating coil in a magnetic field depends on four factors: magnetic flux density $B$, area of the coil $A$, number of turns N and frequency f of rotation. Use Faraday's Jaw to explain why the magnitude of the induced e.m.f. must be proportional to each of these quantities.

Use the ideas in the previous topic to explain what happens if $\mathrm{a}$ you stop pushing the magnet towards the coil shown in Figure and $\mathrm{b}$ you pull the magnet away from the coil.

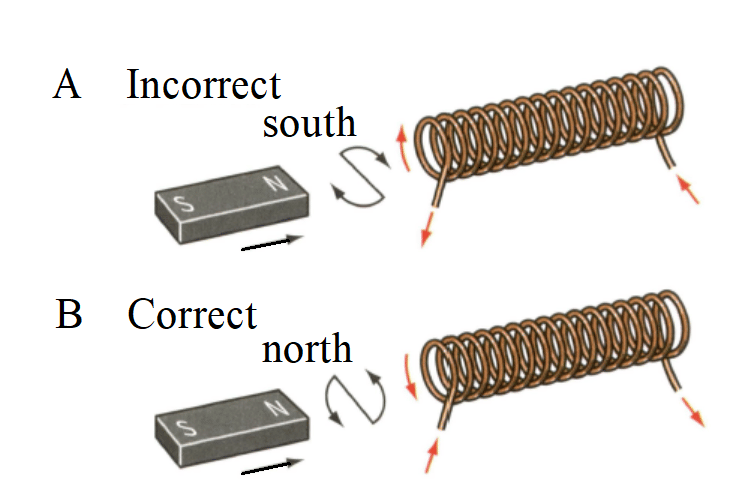
Moving a magnet towards a coil: the direction of the current caused by the induced $e,m,f,$. is as shown in $b,$ not $a,$

Figure, shows a search coil with$2000$ turns and cross-sectional area $1.2 c{m}^2$. It is placed between the poles of a strong magnet. The magnetic field is perpendicular to the plane of the coil. The ends of the coil are connected to a voltmeter. The coil is then pulled out of the magnetic field, and the voltmeter records an average induced e.m.f. of$0.40V$ over a time interval of $0.20s.$
Calculate the magnetic flux density between the
poles of the magnet.

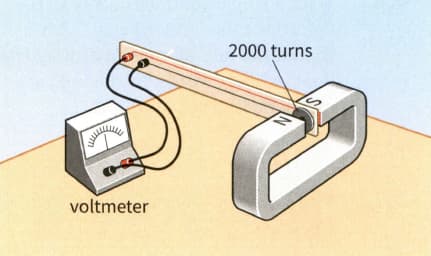
Using a search coil to determine the magnetic flux density of the field between the poles of this magnet.

A wire of length $10 cm$ is moved through a distance  of$2.0 cm$ in a direction at right angles to its length in the space between the poles of a magnet, and perpendicular to the magnetic field . The flux density is $1.5 T$ If this takes $0.50 s,$, calculate the magnitude of the average induced e.m.f. across th ends of the wire.

$A$ conductor of length $L$ moves at a steady speed $v$ at right angles to a uniform magnetic field of flux density $B$.  

Show that the magnitude of the induced $e.m.f. E$ across the ends of the conductor is given by the equation$: e=BLv$.